Le ultime vicende politiche italiane, la Brexit, le scelte commerciali di Trump e il rallentamento economico mondiale hanno scosso nuovamente i rendimenti dei titoli sovrani. L’idea che i mercati siano oramai globali e connessi è comunemente accettata, tuttavia non sempre è facile quantificare il grado d’interconnessione. L’analisi che andremo a illustrare ci permetterà di rilevare come, nel mercato dei titoli di Stato, vi siano shock esogeni che colpiscono alcuni Stati più di altri, mentre alcuni presentano quella che potremmo definire indipendenza sistemica, in altre parole una dinamica scollegata dagli eventi esterni e afferente esclusivamente alle caratteristiche idiosincratiche dello Stato (in gergo tecnico si parla appunto di rischio idiosincratico).
Il campione che abbiamo utilizziamo comprende i cinque paesi UE a più alto PIL (Germania, UK, Francia, Italia, Spagna) più Olanda, Belgio, Portogallo e USA in quanto, come si noterà poi, gli Stati Uniti rappresentano un player determinante all’interno del network europeo.
Al fine di rappresentare lo stato attuale delle interconnessioni che compongono il mercato dei titoli governativi della nostra “rete”, abbiamo utilizzato il metodo di misurazione delle connessioni utilizzato da Diebold e Yilmaz[1], il quale si basa sulla scomposizione di varianze tramite Vector Autoregressive Model e successiva rappresentazione grafica delle correlazioni tra le variabili attraverso nodi e vettori. Questa metodologia, sviluppata nel 2011, ha come obiettivo quello di analizzare l’intensità delle relazioni che s’istaurano all’interno di un campione di elementi omogenei (prezzi azionari, materie prime, prodotti energetici, rendimenti obbligazionari, ecc.) e la concentrazione del sistema nel suo complesso. Sarà infine eseguita un’analisi dinamica[2], volta a monitorare l’andamento dell’indice di connessione del network nel tempo, la quale rifletterà le ripercussioni geo-politiche ed economiche avute negli anni sullo stesso.
Benché solitamente si usi modellizzare i log-rendimenti calcolati sui prezzi, la nostra serie storica di partenza è quella dei tassi zero coupon a maturity costante dieci anni[3]. La scelta è dovuta al fatto che una serie storica dei prezzi dei bond governativi avente tale caratteristica non è di fatto disponibile. Tuttavia, è possibile ottenere la serie dei log-rendimenti artificialmente tramite la differenza dei tassi zero-coupon. Questo è evidente poiché la serie è a maturity costante e che i log-rendimenti equivalgono a:
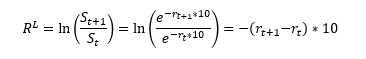
dove S è il prezzo dello zero coupon e è il tasso zero coupon. Il segno meno è espressivo del fatto che se da un giorno all’altro il tasso zero coupon sale, allora il prezzo del titolo scende e dunque il log-rendimento è negativo (RL<0) .
Senza voler scendere troppo nei dettagli, la procedura che abbiamo utilizzato consiste nello stimare la volatilità storica sui log-rendimenti giornalieri, per la quale abbiamo usato un GARCH(1,1), e successivamente nel calcolare le correlazioni che sussistono tra i prezzi/ tassi dei titoli governativi del campione applicando un VAR(3) sulle volatilità così ottenute[4].
Questo approccio di tipo econometrico ci permette di rilevare l’impatto che, uno shock di tipo idiosincratico (per esempio un evento politico) avvenuto nel paese A, ha sul paese B. L’obiettivo è, appunto, quello di misurare l’effetto che uno shock sulle volatilità di A ha sulla volatilità dei tassi zero coupon del paese B. Dall’applicazione di tale metodologia si giunge al seguente risultato:
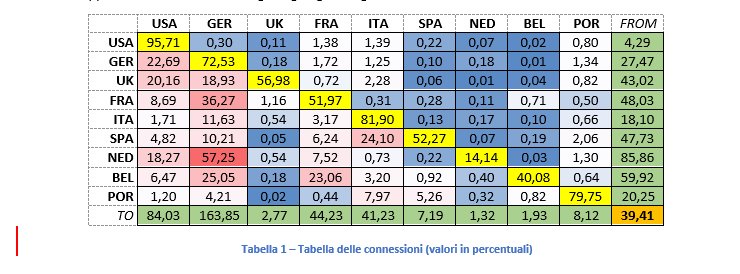
La matrice può essere letta sia per riga sia per colonna. Per colonna sono riportati gli shock che ciascun Paese trasmette agli altri Stati del Network: la colonna GER evidenzia l’impatto che uno shock avvenuto sul mercato dei titoli governativi tedeschi ha su USA (=0.30%), UK(=18.93%) e così via.
Analogamente, leggendo la tabella per riga si può individuare l’impatto che lo Stato, cui la riga si riferisce, riceve dagli altri Stati del Network: se prendiamo la riga FRA, questa ci riporta l’influenza che USA(=8.69%), e GER(=36.27%) hanno sulla Francia, quindi gli shock da questo ricevuti.
La diagonale è molto rilevante poiché rappresenta il livello di volatilità idiosincratica, ovvero quella volatilità che è dovuta a vicende interne, dunque scollegate da dinamiche internazionali.
Esemplificativo è il caso degli USA che, a causa della rilevanza delle politiche della FED e della potenza del Dollaro, subisce scarsamente le dinamiche internazionali (ciò si deduce da un valore della cella USA:USA particolarmente rilevante), bensì le detta, come dimostrato dall’elevato valore della cella TO.
Con riferimento all’Italia, anche il Belpaese, probabilmente a causa delle sue peculiari questioni di politica interna, presenta un’elevata volatilità idiosincratica piuttosto che esogena (la cella ITA:ITA presenta un valore molto alto).
La colonna FROM, invece, indica la volatilità che ogni Stato riceve dal sistema nel suo complesso e si ottiene sommando per riga i valori ivi riportati, ad eccezione di quello della diagonale[5]. Infine la riga TO rappresenta l’intensità con cui un paese contribuisce alla volatilità globale del network e si calcola come la somma per colonna, senza considerare lo shock idiosincratico. L’intersezione fra TO e FROM si può interpretare come il livello di volatilità sistemica del network e si ottiene come valore medio di contribuzione di ogni paese nel trasmettere o ricevere shock di volatilità dall’esterno (valore medio riga TO o FROM).
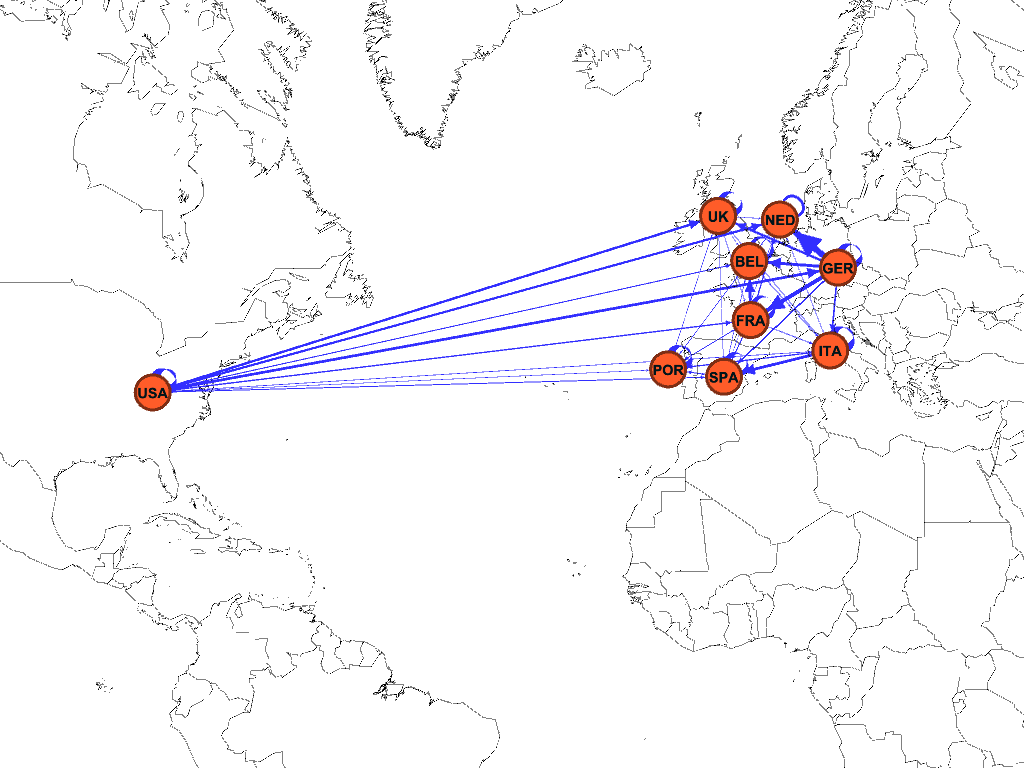
Figura 1: Network e Interconnessioni.
Con l’ausilio grafico del network[6],
rappresentato nella Figura 1, possiamo meglio commentare i valori della Tabella 1.
Germania e USA si presentano come i maggiori contributori alla volatilità del
sistema; molto forte in particolare è l’influenza della Germania sui paesi dell’area
centro-europea (Olanda, Belgio, Francia). Il ruolo degli USA rimane comunque
prevalente se si osserva che la Germania condiziona il mercato americano per lo
0.30%, mentre gli USA influenzano la Germania per un valore pari al 22.69%.
Il Regno Unito si presta a essere influenzato dal Treasury americano e dal Bund
tedesco e non risulta capace di condizionare nessun paese del Network, probabilmente
a causa di diverse dinamiche monetarie/ inflazionistiche rispetto al blocco
Europeo e agli USA.
L’Italia, come detto, risulta poco correlata (il valore della colonna FROM è il
più basso dopo quello degli USA) a causa del suo elevato rischio
idiosincratico. Il suo contributo al rischio sistemico (riga TO) tuttavia è il
quarto più alto, indice che il mercato dei BTP è comunque in grado di influenzare
il network complessivo. Nonostante ciò, questa influenza sembra dirigersi esclusivamente
verso i paesi periferici, in particolare la Spagna: probabilmente questo
fenomeno è dovuto al fatto che i futures sul Btp italiano sono, per questioni
di maggiore liquidità rispetto ai futures iberici, utilizzati dagli operatori
dei paesi periferici per l’hedging delle loro posizioni.
Infine, nella figura 2 è possibile osservare l’evolversi nel tempo del rischio sistemico
del network inteso come la distribuzione nel tempo dell’indice di connessione,
ovvero del valore della cella arancione della Tabella 1. Si
rileva come, dopo la crisi del 2008, la correlazione totale dei prezzi/ tassi
dei titoli di Stato sia stata particolarmente volatile: si passa da una serie
di movimenti ondulatori di media ampiezza tra il 2011-2014, periodo della crisi
greca e degli Stati periferici dell’UE[7], a un
unico ciclo particolarmente lungo, iniziato nel 2014 e terminato a fine 2017. Questo
periodo è stato scaturito da un notevole incremento dell’indebitamento pubblico
causato dall’attuazione di una serie di piani per il salvataggio degli istituti
di credito più in difficoltà, portati sull’orlo del default da un’elevata
numerosità di sofferenze creditizie, soprattutto in Italia. Altri eventi
rilevanti sono stati la Brexit (rappresentata dai due picchi individuati in
data 2016: il voto a giugno e il crollo della sterlina a settembre), la
drastica caduta del prezzo del greggio, l’avvento dei populismi e
dell’euroscetticismo, i quali hanno generato ondate di volatilità sui mercati e
incertezza, comportando anche un incremento degli spread tra i titoli di stato
dei vari Paesi e il Bund. Nel 2018, le politiche commerciali protezionistiche
di Trump, i problemi all’interno dei paesi OPEC e i disaccordi con gli USA, la
gestione dell’uscita del Regno Unito dall’Unione Europea e la crisi diplomatica
tra Stati Uniti e Cina hanno fatto rialzare l’indicatore del rischio sistemico
a livelli allarmanti. Tuttavia, oggi il valore di tale indicatore sembra
essersi parzialmente stabilizzato, trainato probabilmente dal rally dei listini
globali.
Le ragioni che si nascondono dietro il livello d’interconnessione di una rete sono sicuramente molteplici. Ciò che sembra emergere però è il fatto che in periodi di stress, o comunque di alta volatilità, il livello di rischio sistemico sembra incrementare. La conclusione non banale che se ne può dedurre è quella dell’esistenza di cluster di correlazione, ovvero periodi temporali dove un numero significativo di titoli, tipicamente caratterizzati da dinamiche proprie, si muovono nella stessa direzione, aumentando il rischio di un eventuale “effetto domino”. Come i cluster di volatilità[8], la cui presenza è un fenomeno ben noto nei mercati finanziari, così certi picchi visibili nel livello di rischio sistemico (in figura 2) potrebbero essere spiegati dall’esistenza dei cluster di correlazione. In situazioni di stress, infatti, investitori professionali e istituzioni finanziarie potrebbero essere portati a liquidare massicciamente un ampio ventaglio di titoli da loro detenuti, comportando un incremento della correlazione e dunque del rischio sistemico.
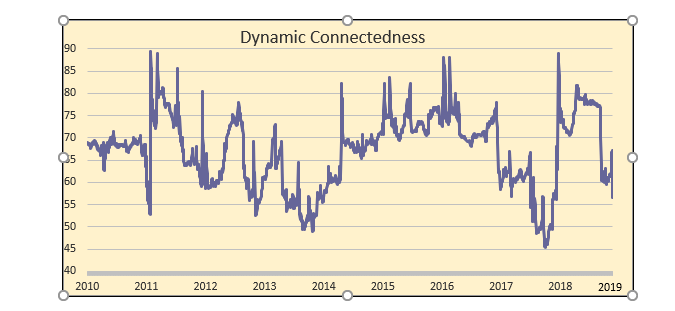
Figura 2: Rischio sistemico del Network (Analisi dinamica)
[1] Diebold Yilmaz, On the network topology of variance decompositions: measuring the connectedness of financial firms, National Bureau of Economic Research, Cambridge (MA), October 2011.
Tramite una metodologia di rolling si suddivide il campione di analisi in sotto-campioni di ampiezza pari alla lunghezza delle finestre temporali definite a priori (nel nostro caso, 175 giorni)
[3] Le rilevazioni vanno dal 2010 al 2019, osservazioni giornaliere
[4] I valori missing del campione in input sono stati eliminati tramite listwise deletion data la loro scarsa numerosità (circa il 2% del numero di osservazioni totali del dataset)
[5] La somma di tale valore con quello della diagonale deve dare 100%: così è possibile verificare il grado di dipendenza dello Stato al sistema (un elevato valore della colonna FROM rappresenta un livello significativo di connessione col network, segno di come tale Paese possa essere indebolito da un qualsiasi evento avverso esterno)
[8] Si definiscono così dei periodi temporali in cui la volatilità di un certo giorno è positivamente correlata alla volatilità dei giorni precedenti. Detto in altro modo, la probabilità che la volatilità sia alta (bassa) è maggiore se nei giorni che precedono la volatilità è stata alta (bassa).



