Executive Summary
In data 31 marzo il Basel Committee on Banking Supervision ha presentato il final standard dal titolo ”The standardised approach for measuring counterpary credit risk exposure” [1]. Il documento inerente ad un approccio non dipendente da scelte di modello [Standardised Approach (SA)] per misurare l’esposizione in caso di default per il counterparty credit risk (CCR). Si tratta sempre di un tema di valutazione dei derivati, come per il documento sugli AVA di EBA uscito nella stessa data, e di cui si è parlato in [7,8]. Mentre però il tema AVA riguarda le valutazioni di bilancio, e di conseguenza l’applicazione di filtri sul patrimonio, in questo caso la grandezza di interesse è l’EAD (Exposure At Default), cioè il valore che potremo definire ”medio prudente” del derivato, quindi del credito, nello scenario di un possibile default lungo l’orizzonte temporale 0-1 anno del framework di Basilea. Il nuovo approccio standardizzato (SA-CCR) sostituisce sia l’attuale metodo dell’esposizione corrente (CEM) che il vecchio ”metodo standard” (SM) nel quadro di adeguatezza patrimoniale, e sarà operativo dal 1 gennaio 2017.
1 Quadro Attuale
Se la disciplina degli AVA è in qualche modo “nuova”, è utile inquadrare lo Standardized Approach per il counterparty risk all’interno delle tassonomie del framework di Basilea e delle evoluzioni storiche. Procediamo quindi con alcuni punti salienti:
- il rischio di controparte (CCR) , inteso in senso stretto, riguarda il default della controparte a scadenza, e quindi il rischio che un Mark to Market (MtM, si noti che nell’uso fair value e MtM sono pressoché sinonimi) positivo per la banca, quindi una esposizione creditizia, non venga riscosso. Pertanto, nelle componenti di rischio del I pilastro di Basilea, e relativi vincoli di dotazione patrimoniale, il CCR appartiene al Rischio di Credito.
- la tipicità del CCR rispetto alla generale categoria di appartenenza è la complessità della stima della EAD, cioè del MtM corrente nel momento dell’eventuale default. La maggiore complessità è legata sia alla stocasticità delle evoluzioni future dell’esposizione creditizia (si pensi per confronto al piano di ammortamento deterministico di un mutuo) sia al fatto che in un derivato (e.g. uno swap) o in un portafoglio di derivati la banca e la sua controparte possano alternarsi nel tempo nel ruolo di creditore e di debitore, in relazione al fatto che il MtM abbia segno positivo o negativo
- nel framework di Basilea, il requisito patrimoniale R per il rischio di credito (e quindi anche per il rischio di controparte) si calcola – per le banche che utilizzano modelli interni – con la funzione di ponderazione, quindi R = EAD ´ LGD ´ f (PD,M,r). In tale funzione (si veda [4] per comprenderne il significato) i parametri di maturity M e correlazione r sono assegnati dal comitato, mentre le banche stimano con propri modelli le probabilità di default PD e loss given default LGD. Per le banche che non utilizzano modelli interni in modo più semplice si ha R = EAD ´ FC ´ FP ´ 8%. Il fattore di conversione creditizia FC e il fattore di ponderazione FP riflettono mediante griglie tabellari il rating della controparte e caratteristiche del prodotto e delle sue garanzie. Per motivi di spazio rimandiamo alla Circolare 263 di Banca d’Italia per tutti i dettagli.
- la validazione del rischio di controparte consiste nella autorizzazione da parte della banca centrale (Banca d’Italia fino a ottobre 2014, BCE nel seguito) concessa alla banca di potere usare modelli interni per la determinazione della EAD ai fini del calcolo del requisito R. A oggi vi sono in Italia due banche in corso di validazione, molte meno di quanto è avvenuto sul rischio di mercato o sul rischio di credito “generale”, per la complessità della materia e i vantaggi patrimoniali (i.e. riduzione di R) limitati o di difficile quantificazione
Quanto sopra è il punto di partenza. In Basilea 2 (e anche in Basilea 3, fino alla data di decorrenza del nuovo framework), la determinazione della EAD segue 3 diversi metodi.
Il primo e largamente più diffuso è il metodo delle esposizione corrente (CEM – Current Exposure Method), per cui si ha che
EAD = Max(MtM,0) + Add-On
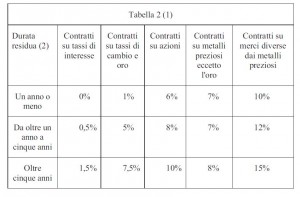
Viene quindi prudenzialmente applicato un vincolo di non negatività al MtM corrente, e poi si applica un add-on per tenere conto di possibili evoluzioni future che possano far aumentare l’esposizione. L’add-on deve essere quindi agganciato alle volatilità tipiche dell’underlying e del payoff. Riportiamo qui la tabella delle percentuali del nozionale con cui si calcola l’add-on.
Il secondo metodo, detto metodo standard (SM), poco utilizzato, si basa su greche e sensitivities, cioè su profili di evoluzione del MtM approssimato mediante scenari conservativi sui fattori di rischio (underlying, tassi risk-free, …) e mediante sensitivities dell’impatto su MtM futuri.
Infine il metodo dei modelli interni prevede il calcolo dell’EPE, Expected Positive Exposure, una media probabilistico-temporale delle evoluzioni future del MtM, irrobustita da vincoli conservativi di non decrescenza nel tempo dei profili del MtM.
Si tratta di un calcolo molto complesso nel senso dello sforzo computazionale, perché richiede in sostanza di valutare MtM in molti time buckets futuri e ancora più numerosi scenari simulati. Si veda [5].
2 Il nuovo assetto SA-CCR
Il paper 279 [1] del comitato di Basilea è frutto di un percorso lungo quasi un anno, iniziato con il paper 254 [2].
Scopo generale di questa importante revisione è quello di eliminare il metodo standard (SM) e di trasformare il modello CEM in un modello maggiormente risk sensitive, nel senso di:
a) determinare in modo più preciso le possibili evoluzioni del MtM;
b) tenere conto in modo più accurato degli accordi di collateral e netting diffusi sul mercato.
Nel paper 254 il nuovo metodo era definito NIMM, Non-Internal-Model-Method, ora modificato in SA, Standardized Approach.
Il punto di partenza generale è dato dalla formula:
EAD = alpha * (RC + PFE)
dove:
- alpha = 1.4 è un fattore conservativo previsto anche nell’approccio EPE;
- RC = replacement cost, tiene conto del valore corrente (MtM), con vincoli di non negatività, e del valore del collateral detenuto e degli accordi di compensazione e marginazione;
- PFE = potential future exposure, incorpora in modo rigoroso e prudente, e più realistico dell’add-on, la volatilità futura del MtM.
Se sul piano definitorio è tutto piuttosto semplice, l’impianto di calcolo effettivo stabilito dal paper è viceversa molto articolato, specie per la componente PFE.
Ci limitiamo a evidenziare alcuni punti fondamentali riguardanti il PFE:
- i deals sono attribuiti a 5 diverse asset class: equity, interest rate, forex, commodity, credit;
- a livello di deal (trade level nel linguaggio del comitato) si effettuano le seguenti trasformazioni: notional ® adjusted notional ® effective notional, mediante un supervisory delta;
- infine all’effective notional si applica un supervisory factor SF (concettualmente simile agli add-on del CEM) per ottenere il PFE.
Tutto quanto sopra sarebbe semplice se una banca avesse un singolo deal, quindi appartenente, ad esempio, a una singola asset class, o a un singolo accordo di collateral – in altri termini se ogni calcolo fosse a un solo “livello”. Nella realtà si deve tenere invece conto di numerosi passi in cui si effettuano i calcoli e le relative aggregazioni/compensazioni. Tra il livello più alto, asset class, e il trade, sono previsti (almeno) gli hedging set e le categories, all’interno dei quali le aggregazioni delle posizioni hanno metodi diversificati.
Nel caso equity, ad esempio, è previsto un singolo hedging set ed è permessa una perfetta compensazione dell’effective notional (di fatto, si tratta del delta equivalent) all’interno dello stesso single name azionario, con applicazione però di un modello con rischio sistematico e specifico a 1 fattore per aggregare, mediante opportune correlazioni, le posizioni. Con ulteriori differenze tra strumenti azionari vs. indici e fondi.
Nel caso interest rate è invece previsto un hedging set per ogni diversa valuta (USD, EUR, GBP), e ognuno di essi è diviso in 3 maturity buckets: inferiore a 1 anno, fra 1-5 anni, e superiore a 5 anni. Tra diversi maturity buckets, un parziale off set è ammesso in base a ulteriori formule.
Tra diverse asset class e verso diverse controparti non è ammessa alcuna compensazione, quindi in modo conservativo la EAD globale del portafoglio si forma con approccio building block come somma delle quantità per asset class / controparte.
Per tenere conto in modo più preciso del rischio effettivo, sono previsti una serie di fattori di correzione e di bounds all’interno delle formule per tenere conto del MPOR, Margin Period of Risk, cioè delle frequenze di marginazione sugli accordi di collateral, e per impedire che il risultato finale sia inferiore al modello interno EPE, che determinerebbe un disincentivo allo sviluppo di tali modelli.
Da ricordare che il nuovo framework ha alcuni effetti anche per i modelli interni di classe EPE: è infatti abrogato lo short cut method, su cui alcune banche medio grandi italiane si erano orientate forse con troppa rapidità, che consente di stimare l’esposizione futura in base alle statistiche degli MtM passati, senza obbligo di full revaluation dei deals.
3 Impatti e punti critici
In generale, un qualunque modello di classe standard dovrebbe cercare un buon trade-off tra la sua semplicità, per potere essere adottato anche da banche con risorse sul risk management e sui sistemi informativi limitati, e la proprietà di essere risk sensitive, cioè determinare figure di rischio e di requisito patrimoniale R di ampiezza effettiva rispetto ai rischi nei portafogli.
Dalla sua prima versione nel paper 254, il nuovo modello ha raccolto diverse critiche, evidenziate dai diversi contributi nella fase di consultazione, sia da singole banche sia da associazioni di categoria e internazionali, sia veda come esempio [3].
Tra i diversi punti deboli, si evidenzia già il primo step, vale a dire il mapping verso una asset class. Vi sono nel mercato diversi prodotti ibridi, cioè dipendenti da un paniere per esempio di divise e azionario. L’attribuzione al fattore di rischio primario è accettabile come principio (paragrafo 152), ma di applicazione non ovvia nella pratica. Oppure la specificazione ancora approssimativa di un rischio importante, come il rischio di volatilità (vega). Se infatti il paper 254 rinviava alla consultazione la tematica, il nuovo paper, paragrafo 163, indica in modo molto sintetico che il supervisory factor SF per calcolare l’add-on debba essere 5 volte rispetto a quello delle stessa asset class riferito al rischio usuale sul sottostante. In concreto, un variance swap azionario dovrebbe avere un fattore 5 volte maggiore della corrispondente opzione azionaria plain.
Ricordiamo che il MtM di un derivato si può modificare in modo rilevante anche solo per modifica delle volatilità di mercato e a nostro parere il nuovo approccio attuale SA-CCR avrebbe dovuto meglio trattare la fattispecie.
Altre fragilità illogiche sono state risolte nella fase consultiva. Nella determinazione della esposizione (delta equivalent) verso un underlying mediante moltiplicazione tra nozionali adjusted e delta, era previsto un delta pari ai valori {0.5, -0.5}, cioè dei soli casi at the money per una loro (presunta) maggiore rischiosità, e quindi incorporare in modo corretto solo il segno lungo/corto del deal. Tale vincolo è stato rimosso e ora le banche useranno i delta effettivi presenti nei sistemi, anche se una formulazione di delta in termini di sensitivity del I ordine model-independent, sarebbe stata preferibile rispetto alla citazione della formula di Black&Scholes, ovviamente non applicabile per tutti i possibili pay-off.
Riassumendo, il calcolo SA è in ogni caso molto impegnativo, perché richiede alle banche di effettuare processi di calcolo (e mantenere aggiornati dati anagrafici e di rischio) lungo numerosi livelli, che riportiamo in ordine top-down:
- controparte
- netting agreement
- asset class
- hedging set
- category
- deal-underlyng
- componenti dell’underlying.
Pur apparendo lontana la scadenza del 1 Gennaio 2017, questo nuovo framework obbligherà ad usare strumentazioni ben più raffinate di quanto serve ora per il calcolo degli add-on, vale a dire la banale segmentazione della tabella riportata in Sezione 1. Si possono prevedere pertanto dal 2015 attivazione di progetti ad hoc e gruppi di lavoro.
Appare infine difficile prevedere se il nuovo SA, a parte un uso per obblighi di calcolo di R, entrerà nei monitoraggi gestionali del rischio, per come appare lontano nei suoi step di calcolo dalla variabili driver usate nel trading operativo (MtM, greche, ..)
Tra gli aspetti positivi, va senz’altro citato che il nuovo approccio SA si inquadra in un percorso internazionale dove tra diverse regolamentazioni, o tra diversi regulators, si cerca una definizione comune e uniforme di alcuni principi guida. Per esempio, le asset class del counterparty risk hanno forti punti di simmetria con la normativa EMIR sui trade repository e con la fundamental review del trading book in corso di analisi da parte del comitato di Basilea (paper 265 [6]). Ribadiamo infine che la formulazione del SA, che bene tiene conto dei margini a garanzia e dei diversi accordi di collateral, permette di estendere la determinazione di EAD anche ai derivati quotati, in accordo con i requisiti di capitale previsti verso le controparti centrali (CCP).
Riferimenti
[1] Basel Committee on Banking Supervision (2014) The standardized approach for measuring counterparty credit risk exposures
[2] Basel Committee on Banking Supervision (2013) The non-internal model method for capitalising counterparty credit risk exposures
[3] BNP Paribas (2014) BNP answer to BCBS254
[4] Basel Committee on Banking Supervision (2005) An Explanatory Note on the Basel II IRB Risk Weight Functions
[5] M.Pykthin (2009) “Modeling credit exposure for collateralized counterparties”, The Journal of Credit Risk.
[6] Basel Committee on Banking Supervision (2013) Fundamental review of the trading book: A revised market risk framework
[7] M. Bonollo, D. Marazzina (2014) Prudential Valuation dei derivati (AVA). FinRiskAlert.it
[8] M. Bonollo, D. Marazzina (2014), AVA: Quali novità per la Prudential Valuation. FinRiskAlert.it