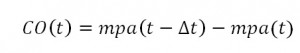Nelle best practices di gestione della liquidità e dei rischi finanziari l’utilizzo di modelli economico-statistici basati su variabili legate al comportamento della controparte (i c.d. “modelli comportamentali”) sta assumendo una diffusione rilevante ed in costante crescita nel tempo.

Tra i modelli comportamentali che si collocano all’interno delle pratiche di Asset Liability Management (ALM), il modello Bond Portfolio Replication (o modello Bond Replica) rappresenta uno degli approcci più conosciuti ed utilizzati nel contesto bancario europeo ed internazionale per la gestione delle poste a vista.

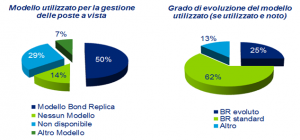
Una recente indagine riguardo al modello usato per la gestione delle poste a vista, effettuata su un campione di grandi banche italiane, testimonia infatti come esso venga utilizzato, nella sua forma più generale, da almeno la metà degli istituti. Solo il 25% di questi, però, lo utilizza in una versione più evoluta di quella standard, in cui al modello classico vengono aggiunte modifiche che rendono il modello più preciso e/o più adatto a descrivere le specifiche caratteristiche delle singole banche.

La principale finalità-obiettivo del modello è consentire una gestione dinamica della liquidità generata dalla raccolta senza scadenza contrattuale (c.d. poste a vista) in modo da garantire che:

–          l’ammontare di masse depositate dai clienti sia ripartito, in coerenza con i sottostanti rischi, su un arco temporale più ampio della scadenza a vista (overnight);

–          l’impiego della risultante liquidità disponibile sia canalizzato su impieghi o investimenti a termine che assicurino profitti maggiori facendo leva sui differenziali dei tassi di interesse.

In termini pragmatici, ciò che tale strumento fa è la trasformazione dell’ammontare di poste a vista in un portafoglio di poste a scadenza.

Il Modello Bond Replica consta di due parti fondamentali, trattate in primis in maniera disgiunta ma, successivamente, coniugate tra loro: l’analisi dei tassi e l’analisi dei volumi.

Figura 1: Survey sul Modello Bond Replica. Campione di 14 banche italiane.

Analisi dei tassi

La prima parte del modello, nella sua versione più classica, riguarda l’analisi delle serie storiche dei tassi. Tale studio si sviluppa a partire dall’ipotesi che esista una relazione tra l’andamento del tasso di mercato e quello dei depositi. In particolare, tale legame viene studiato attraverso un modello econometrico con correzione d’errore ECM (Error Correction Model), che si compone di due distinte relazioni: una di lungo periodo (c.d. “relazione di equilibrio”) ed una di breve periodo (c.d. “dinamica”).

Attraverso l’ECM la deviazione dello stato attuale rispetto alla relazione di lungo periodo viene progressivamente assorbita sulla base della relazione dinamica di breve periodo. Tale procedimento non consiste in un modello che ne corregge un altro, bensì in un modello che permette di stimare in maniera diretta la velocità alla quale la variabile dipendente (nel caso in questione, il tasso dei depositi) tende all’equilibrio a seguito di un cambiamento nella variabile indipendente ([1]).

L’obiettivo principale di questa analisi è quello di individuare una parte dei depositi che sarà sensibile all’andamento dei tassi (la cosiddetta parte elastica) ed una che ne sarà invece indipendente e non risentirà di eventuali shock di mercato. La relazione di lungo periodo fornisce una misura di quanto le variazioni del tasso di mercato si riflettano in variazioni del tasso di deposito:

dove   rappresentano, rispettivamente, il tasso delle poste a vista e il tasso di mercato.

Tramite regressione lineare con metodo dei minimi quadrati sui dati storici è possibile stimare i coefficienti   .

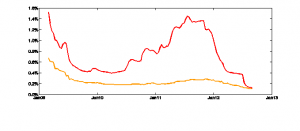
Figura 2: Esempio esplicativo. Serie storiche dei tassi di una delle principali banche italiane. In arancio il tasso depositi, in rosso il tasso Euribor a 1 mese.

Per quanto accurata, la relazione di lungo periodo non è però in grado di descrivere alcuni fenomeni economici quali la velocità con cui i tassi di deposito si adeguano a quelli di mercato e l’asimmetria (vischiosità) con cui avviene tale adeguamento. A tal proposito si introduce quindi, come anticipato, la relazione di breve periodo, espressa dalla seguente formula:

che permette di stimare, tramite i coefficientiil tempo necessario affinché la componente       dei tassi di deposito sensibile alle variazioni dei tassi di mercato si allinei al valore determinato dalla relazione di lungo periodo, caratteristica utilizzata in sede di coniugazione del modello dei tassi con quello dei volumi.

Analisi dei volumi

Lo scopo del modello dei volumi è quello di stimare il possibile andamento futuro dei volumi delle poste a vista a partire dalla serie storica. Tale previsione viene fatta in maniera prudenziale, supponendo cioè il verificarsi di una eventuale crisi di liquidità con impatti sfavorevoli per la banca.

Inizialmente si scompone, con l’ausilio di un filtro statistico (Hodrick-Prescott), la serie storica dei volumi dei depositi in una componente stabile (detta Core) – che si ottiene togliendo all’ultimo dato disponibile sui depositi la quantità corrispondente alla “massima componente volatile osservata in passato” (in termini assoluti) – ed una volatile (c.d. Non core). Il tutto viene poi espresso in termini percentuali rispetto all’ammontare totale.

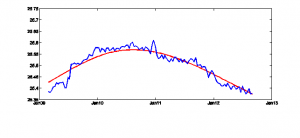
Figura 3: Esempio esplicativo. Applicazione del filtro statistico alla serie storica dei volumi logaritmici. In blu la serie storica, in rosso lo smoothing effettuato dal filtro.

Una volta individuate tali quantità si identifica un profilo di persistenza, il cosiddetto profilo dei volumi minimi probabili (mpa), che descrive come la componente core decresca all’allontanarsi della data di analisi. Considerando t = 0 l’istante in cui viene effettuata l’analisi, il profilo degli mpa, in accordo con gli studi degli istituti finanziari analizzati, è definito dalla seguente funzione:

 

In tale equazione,               è la deviazione standard della componente ciclica (volatile) identificata dal filtro, mentre   è il valore della distribuzione normale standard in corrispondenza di un livello di confidenza pari ad  ;  rappresenta il logaritmo dei volumi attuali. Il profilo dei volumi minimi probabili si annullerà all’istante , data in cui si suppone si collochi la maturity di queste poste senza scadenza. Esso rappresenta il comportamento dei volumi dei depositi futuri e verrà utilizzato per la programmazione del piano di impiego/investimento della liquidità generata da tali poste di raccolta.

Coniugazioni dei modelli

A partire dal profilo dei volumi minimi probabili è possibile quindi identificare un piano di impiego seguendo una logica affine alla strutturazione di un portafoglio di titoli con varie scadenze. Più precisamente, il profilo è una funzione deterministica del tempo che esprime l’ammontare dei depositi totali posseduti in futuro nello scenario considerato.

Supponendo una curva dei tassi a termine crescente nel tempo (in condizioni normali del mercato il tasso di interesse cresce all’allontanarsi della maturity) è più vantaggioso investire un ammontare di denaro in un titolo con un time to maturity più lontano possibile guadagnando così maggiormente grazie ad un tasso di interesse più alto, ma in modo tale da poter essere sufficientemente tranquilli che non si avrà bisogno di tale quantità liquida fino a quel momento.

In termini matematici, facendo riferimento alla formula riportata di seguito, dato un generico istante temporale          , l’ammontare che si investirà è rappresentato dalla differenza dei volumi dei depositi che si prevede saranno ancora disponibili al tempo   e quelli all’istante  .

Il piano di investimento è descritto dalla cosiddetta curva di liquidità, che chiameremo  , ricavata come differenza dei volumi minimi probabili (mpa) ai diversi istanti temporali (avendo cura di applicare la trasformazione inversa a quella logaritmica):

Il modello di analisi dei volumi consente di individuare una behavioral maturity per le poste a vista, ma è solo tramite la sintesi con il modello econometrico di analisi dei tassi che si giunge ad identificarne il profilo di rischio complessivo. L’individuazione delle componenti Core e Non Core realizzata attraverso il modello di analisi dei volumi deve quindi essere coniugata con le misure di reattività del tasso delle poste a vista determinate attraverso il modello di analisi dei tassi.

 

La stima di parametri       significativamente diversi dall’unità implica che una parte  delle masse a vista può essere interpretata come un prodotto il cui tasso risulta anelastico rispetto a variazioni dei tassi di mercato. I tempi e le modalità di adeguamento della parte elastica  ai valori di equilibrio vengono invece descritti dalla relazione dinamica di breve periodo.

Nella practice operativa con cui tale modello è gestito, l’approccio adottato è quello di simulare un possibile shock   (positivo o negativo) nell’andamento dei tassi mercato che si rifletterà in una variazione dei tassi di deposito applicati alla clientela   , raggiunta tramite variazioni   negli istanti successivi allo shock, in base alla relazione di breve periodo.

Con quest’ultimo elemento la preparazione del piano di investimento dei volumi dei depositi è ora completa. La parte del volume complessivo caratterizzata da un’elevata volatilità (componente non core) è assimilata ad un impiego overnight. La componente core viene invece investita in un portafoglio di titoli con scadenze coerenti al profilo di ammortamento individuato in sede di analisi dei volumi.

 

Riferimenti

[1] Robert F Engle and Clive WJ Granger. Co-integration and error correction: representation, estimation, and testing. Econometrica: journal of the Econometric Society, pages 251–276, 1987