Life insurance products are often characterized by a minimum guarantee: the insurance company manages funds guaranteeing a minimum return to policyholders (with profit products).
In a recent paper with Elisa Mastrogiacomo we investigated how the presence of a minimum guarantee affects the asset manager’s strategy assuming that the liability of the insurance company is partially charged to the asset manager, see also Dong He and Kou (2018) and Lin et al. (2017).
Usually, the funds of policyholders are pooled together in a segregated fund, the insurance company manages it in order to refund claims and lapses of policyholders. The company is remunerated through a constant fee, and a fee that depends on the assets under management (AUM) of the fund (asset management fee) or through a share of the surplus over the guarantee in case it is positive and zero otherwise (performance fee). In some cases, a combination of the two schemes is at work.
Life insurance products with a minimum guarantee establish that the insurance company is endowed with a liability in case the fund goes below it. If this is the case, then the insurance company has to refund the performance gap to policyholders and, therefore, the company is short of a put option written on the AUM of the fund. This type of contract affects the management of the segregated fund by the insurance company.
We have investigated the asset management problem in a dynamic setting assuming that the payoff of the asset manager is made up of a constant fee, an asset management/performance fee and the liability in case the performance target is not reached. The guarantee is defined as a threshold on the AUM. We assume that the manager’s remuneration decreases in case the AUM is below the guarantee threshold, concurring to the loss of the insurance company, but it cannot become negative. Therefore, it is the insurance company, with its revenues from other activities or its capital, that ensures the payment of the minimum return to policyholders, while the manager only concurs to the loss in the sense that her remuneration is negatively affected if the minimum guarantee is not reached. We deal with a stochastic and a constant risk interest rate.
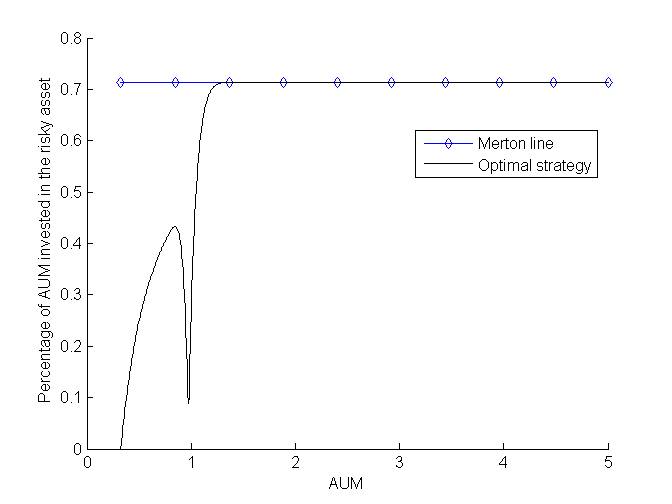
We show that an asset management fee or a performance fee lead to a similar investment strategy with the latter yielding a lower level of risk exposure (investment in the risky asset). We show that the manager may invest in the risky asset even if the put option is in the money, i.e., when AUM are below the threshold of the guarantee. In that region, the investment is hump shaped: when the put option is deep in the money (AUM are far away from the threshold) the manager doesn’t invest in the risky asset; as AUM increase, the investment in the risky asset increases and then decreases just below the guarantee reaching a null investment for a level of AUM that allow to reach the minimum guarantee. At that point there is a kink, then the investment in the risky asset increases again converging towards the solution obtained without constraint in the region where the guarantee is satisfied (Merton solution). The strategy is depicted in the figure below: we consider a market with a risk-free asset (a bond) and a risky asset (a stock), and we plot the percentage of the AUM (1=100%) invested in the risky asset by the manager, setting the minimum guarantee threshold equal to 1.
If the company is remunerated also through a constant fee, then the investment strategy may be hump shaped also above the threshold yielding excess risk taking with respect to the Merton solution. This result confirms that, contrary to common wisdom, a remuneration based on a fixed fee leads to excess risk taking, see Ross (2004) Barucci et al. (2018) .
Bibliography
Emilio Barucci, Gaetano La Bua and Daniele Marazzina (2018) On relative performance, remuneration and risk taking of asset managers, forthcoming in Annals of Finance.
Emilio Barucci, Daniele Marazzina and Elisa Mastrogiacomo (2018) Optimal investment strategies with a minimum performance constraint, working paper.
Xue Dong He, and Steven Kou (2018) Profit sharing in hedge funds, Mathematical Finance, 28: 50-81.
Hogcan Lin, David Saunders, and Chengguo Weng (2017) Optimal investment strategies for participating contracts, Insurance: Mathematics and Economics, 73: 137-155.
Stephen Ross (2004) Compensation, incentives, and the duality of risk aversion and riskiness, The Journal of Finance, 59: 207-225.