Executive Summary

L’avvento dei nuovi reference rate, fortemente voluto in seguito alla crisi di credibilità dei LIBOR, ha portato pressoché per tutte le currency alla definizione di specifici tassi Overnight come nuovi rereference (free risk) rate. Questo determina una forte innovazione in tutti i prodotti bancari e finanziari indicizzati a tali tassi. Nell’articolo aspetti tecnici e problemi aperti.

1 La riforma dei tassi IBOR

Motivazioni e linee guida della riforma dei tassi IBOR mediante la benchmark regulation (BMR) sono già bene descritti in [10], quindi non ci dilunghiamo, soffermandoci sugli aspetti significativi per le parti tecniche delle sezioni successive.

Per ogni currency, si è affermato in questi anni un nuovo reference rate, che opera come il migliore “rappresentante” dei tassi free-risk per l’area valutaria di riferimento.

Su questo punto si è definita una forte differenza tra area Euro e altre valute.

Per l’area Euro, il tasso €STR di tipo overnight ha soppiantato il vecchio tasso EONIA, ma rimane anche il tasso Euribor, con nuova metodologia per cui è definito Euribor Ibrido. In breve, la sua quotazione non dipende solo da un panel di quotazioni di un numero limitato di banche, ma anche anzi con priorità da transazioni osservate sul mercato tra banche e anche con large corporate.

Per le altre aree valutarie, in primis GBP e USD, il nuovo reference rate è costituito sempre da soli tassi di tipo Overnight, rispettivamente SONIA (sterling ovvernight index average) e SOFR (secured overnight financing rate). Tassi cioè che fanno riferimento a operazioni di lending di durata h = 1 giorno.

Inoltre, basandosi su operazioni effettive e non su quotazioni, sono pubblicati in generale in (t+1), mentre gli attuali LIBOR sono pubblicati al tempo (t) per operazioni con decorrenza (t).

Se però usciamo da mercato banche vs. banche e ci riferiamo al mercato delle operazioni tra banche e clientela, sia corporate sia retail, sono altre le durate e le periodicità tipiche. Per i mutui e finanziamenti il piano rateale è spesso mensile, per i bond la cedola è spesso semestrale, ecc.

Quindi il mercato necessita, da sempre, di tassi a termine, cosiddetti term rate, su varie scadenze.

Il fatto però che i nuovi benchmark rate siano tipicamente overnight pone su questo vari problemi, che illustriamo con maggiore dettaglio nelle sezioni successive.

2 Convenzioni sui floating rate. Tassi forward looking e fixing in advance

Come noto, con il termine fixing si intende il processo di fissazione di un valore finanziario, preso a riferimento poi da altri contratti, quali mutui, bond, derivati.

I tassi LIBOR sulle diverse divise, come Euribor per l’area EURO, erano quotati su diverse scadeze, quali  1 settimana, 1 mese, 3 mesi, 6 mesi, 12 mesi.

E fanno riferimento a operazioni con decorrenza in (t), talvolta (t+1) o (t+2).

Indicando con (h) la durata, ci si riferisce pertanto a operazioni, supponiamo di prestito, in cui alla data (t) viene erogato l’importo, in (t+h) viene  restituito maggiorato degli interessi al tasso pattuito, con un calcolo proprozionale al tempo. Indicando quindi con R il tasso e con C il capitale, il valore finale è dato da

V(t+h) =  C ˖ (1 + hR)

Si dice quindi che i tassi quotati sono forward looking, in quanto fanno riferimento nel mercato interbancario a operazioni che nascono nel medesimo istante.

Se pensiamo a un qualunque mutuo indicizzato a tale tasso, si usa dire che il fixing del tasso è in advance, cioè fatto a inizio del periodo di calcolo della rata.

I due aspetti sono fortemente correlati. Sul mercato degli operatori professionali, è natutale che i term rate facciano riferimento a operazioni con decorrenza sincrona alla quotazione. Sul mercato delle operazioni con clienti finanziati o investitori, conoscere il tasso applicato a inizio del periodo della rata o della cedola è la preferenza pressoché universale degli operatori, quindi fixing in advance.

Nulla vieta, ma è un caso scolastico molto raro, che un tasso forward looking sia applicato alla fine del periodo, cioè in arrears. Ma appunto è un caso di frequenza quasi nulla. Esempio: su bond con cedola semestrale luglio-dicembre 2020 si applica il tasso Euribor 6 mesi osservato in data 31 dicembre 2020 (che però fa riferimento a depositi tra banche che si verificano nel primo semestre 2021).

Da queste prime note si intuisce il problema: come possono i tassi overnight, riferiti al periodo h = 1 giorno, funzionare come indice di riferimento per operazioni con periodicità di ben diversa lunghezza, quali soluzioni? Regulators, working group, operatori, stanno convergendo verso nuove regole e preferenze, di fatto una importante evoluzione nelle abitudini, nei processi, nei sistemi informativi, con conseguenze anche a livello legale e di compliance. Nella prossima sezione gli orientamenti alla data, che non costituiscono ancora “lo standard”, ma un framework di ormai prossima applicazione.

Si tenga infatti presente che per alcune aree valutarie il regulator, come Bank of England per la sterlina, sta fortemente premendo per dismettere i tassi LIBOR nelle nuove emissioni e prodotti già dal primo trimentre 2021, quindi  un anno in anticipo rispetto alla cessazione ufficiale dei LIBOR.

3 I nuovi term rate. Compounding in Arrears ?

Su quanto proposto dai vari regulator e gruppi di lavoro internazionali, con ruolo in qualche modo di guida da parte delle aree GBP e USD, si vedano i vari documenti in [3], [4], [5], [6].

La principale proposta è quella verso una metodologia di compounding in arrears, abbastanza innovativa rispetto alla convenzioni applicate in generale su prodotti bancari e finanziari nel “vecchio” mondo degli IBOR.

Vediamo i vari aspetti.

Quanto al compounding, si tratta del principio per cui un investimento overnight può essere replicato giorno per giorno, capitalizzando gli interessi, e quindi l’idea di base è che un tasso di interesse su un tenor maggiore, per esempio un mese, sia espresso in modo più fedele dal compounding rispetto a una media aritmetica. Utile qualche formalismo. Se indichiamo con R(i) il tasso al tempo (i), i = 1…D, e omettendo in quanto non essenziale il capitale iniziale, che possiamo porre C =1, il valore dell’investimento V(D) dopo D giorni è dato da

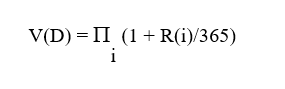
L’interesse maturato totale è pertanto dato da I(D)

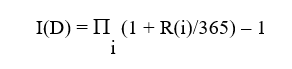
Per riportare il tutto a tasso di interesse annuo, come d’uso nelle quotazioni, basta riproporzionare e si ha

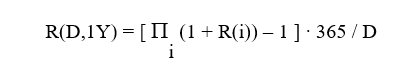
Manca ora un ultimo dettaglio. Poiché negli weekend i tassi non sono quotati, o a causa di festività del mercato di riferimento, uno specifico valore può essere utilizzato per più giornate. I regulator e gruppi di lavoro si stanno orientando verso un peso n(i) = 3 giorni associato al fixing del venerdì. Il tutto si riscrive quindi in modo completo come

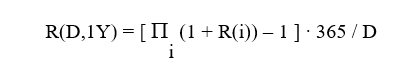
Da un punto di vista tecnico e della matematica finanziaria non è questa una novità. Il tasso composto, il cui limite è costituito dal modello continuo V(t)=V(0)∙exp(rT) è ben noto. Oltretutto una famiglia di derivati molto diffusi come gli OIS, overnight indexed swaps, da sempre determina la componente floating mediante capitalizzazione dei tassi overnight di mercato.

E’ però fortemente innovativo pensare al fatto che anche prodotti molto più retail, quali i mutui con il loro calcolo rata e i bond con le cedole, applichino tale composizone geometrica dei rendimenti. Come osservato nei vari gruppi di lavoro, è questo il calcolo che più rispetta il “time value of money”.

Dopo il problema del QUANTO, cioè di calcolo del tasso su tenor diversi da overnight, partendo da tassi overnight, vediamo la questione del QUANDO o del COME.

Si tenga conto che basandosi su operazioni effettive, i nuovi tassi saranno disponibili e pubblicati in generale in (t+1), con riferimento a (t), dalle banche centrali e dai provider di mercato.

Le banche devono utilizzare questi valori per garantire calcolo e addebito/accredito di cedole, rate, in modo tempestivo rispetto al periodo contabile di riferimento. Per farlo devono però acquisire i fixing, controllarli, propagarli nei sistemi informativi. Non è pensabile di differire, magari di un paio di giorni, operazioni contabili e informativa al cliente a causa delle regole di pubblicazione.

Quindi il calcolo sarà certamente in arrears, cioè di determinazione del tasso di periodo in base ai tassi overnight del periodo appena concluso, ma con alcuni aggiustamenti legati a questa necessità di tempestività di determinazione della quota interessi.

Ci limitiamo per motivi di spazio alle due clausole attualmente più promosse in sede internazionale.

Clausola Lag/Shift

• Definizione: il calcolo è compounded in arrears, con shift di alcuni giorni all’indietro, in modo da deeterminare il tasso di periodo con un maggiore margine temporale
• Esempio. Per il periodo 1 giugno – 30 giugno, con lag pari a L = 5 giorni lavorativi, si provvede al calcolo usando i fixing che si riferiscono al periodo 23 maggio – 23 giugno

Clausola Lockout

• Definizione: il calcolo è compounded in arrears, con congelamento degli ultimi gironi di periodo, in  cui si usa un valore costante pari all’ultimo osservato.
• Esempio. Per il periodo 1 giugno – 30 giugno, con lock out pari a L = 5 giorni lavorativi, si provvede al calcolo compounding usando i fixing che si riferiscono al periodo 1 giugno – 23 giugno, i valori dal 24 giugno al 30 giugno sono sostituiti dal fixing osservato il 23 giugno, che quindi assume un peso maggiore.

4 Alcune riflessioni

Non tutti gli operatori sono soddisfatti e convinti di una migrazione globale dei mercati verso questa logica di tassi backward looking con applicazione in arrears.

Molti pensano che sia più corretto basarsi su tassi forward looking. In questo caso, una volta che vi sia un mercato veramente liquido di strumenti sui tassi overnight, in particolare Future, OIS e Basis Swap, dalle quotazioni di tali strumenti si potrà costruire una curva a termine robusta che si basa su questo new normal.

E’ al tempo stesso dubitabile che tali tassi forward looking, dedotti dal mercato medante un processo di bootstrapping e non legati ale quotazioni dirette come sono invece gli attuali LIBOR, possano essere base di indicizzazione di prodotti quali mutui e bond.

Quindi prodotti e contratti andranno verso queste nuove clausole. Tale evoluzione pone di certo delle problematiche anche sulla compliance relativa alla trasparenza, cioè sulla comunicazione pre contrattuale al cliente delle regole di gestione del parametro di indicizzazione, e di disclosure nelle comunicazioni periodiche ed estratti conto sulla determinazione del tasso periodico. Oltretutto, va ricordato, in presenza di una “meccanica” di trattamento dei dati di mercato non certo di facile assimulazione per tutta la clientela.

Viene da chiederesi se i principi di target market della Mifid2, cioè di matching tra le caratteristiche del cliente, in particolare le sue competenze, con le caratteristiche di complessità dei prodotti, non possa essere un utile punto di partenza anche nell’ambito dei prodotti tipicamente bancari.

Ringraziamenti

Un sentito Grazie a Paolo Cobuccio e Alessandro Santocchi, Iason Ltd,  per il proficuo confronto.

Riferimenti

[1] Financial Stability Board (2014), “Reforming Major Interest Rate Benchmarks “.

[2] Financial Stability Board (2019), “Overnight Risk-Free Rates. User Guide ”

[3] Bank of England (2020),“Supporting risk Free Transition through the provision of compounded SONIA”, Discussion Paper.

[4] ARRC (2019), “Appendix to SOFR Floating Rate Notes Conventions Matrix”.

[5] The Working Group on Sterling RFRR (2020), “Use Cases of Benchmark Rates”

[6] ISDA (2020), “Adoption of Risk-Free Rates:  Major Developments in 2020”, ISDA Research Notes.

[7] Schrimpf A., Sushko V. (2019), “Oltre il LIBOR: introduzione ai nuovi tassi di riferimento”, Paper BIS.

[8] Alternative Reference Rate Committee (2019), “Summary of ARRC’s LIBOR Fallback Language”.

[9] Unione Europea (2016), “Benchmark Regulation (BMR)”, Regulation 2016/1011