
Commodity markets may quote the prices of futures contracts for different maturity dates and different delivery periods. If we select a specific delivery period, we can group the prices at different maturities within a single term structure. The shape of the futures term structure is essential to commodity hedgers and speculators as futures prices serve as a forecast of future spot prices. Futures prices contain the information about futures supply and demand conditions, and, as the maturity date approaches, the prices may either increase or decrease. Moreover, seasonal fluctuations are evident for many commodity prices. In this note, we investigate a Bayesian technique known as Kriging to interpolate prices at maturity dates not directly quoted by the market, by embedding trends and seasonalities and by ensuring no-arbitrage conditions between different delivery periods.
1 Model motivation
The problem of bootstrapping the futures curve, which we analyse in this paper, can be faced with various techniques. However, some considerations make Kriging a particularly suitable choice. First, market data are often noisy as we do not know the exact price of market quotes, but our input consists of bid and ask spread prices. Secondly, as explained in the next sections, the futures contracts are linearly constrained due to the no arbitrage conditions. For interpolation problems with noisy data and linear constraints, as that we are interested in, Kriging models provide robust and accurate results.
2 Term structure of futures prices
We consider futures with the shortest delivery duration (usually one month), and we can evaluate all the other ones by averaging their prices. In the following note, we will often use as an example the futures contracts on TTF natural gas[1], which are usually quoted with a delivery period ranging from one month to one year. We associate to each contract a maturity date calculated as the minimum between the last trading date and the first notification date. According to our definition, futures may be quoted after the maturity date, if the first notification precedes the last trading date. We are not interested in futures prices during such period. We define the term structure of futures prices observed at t with one-month delivery period as the curve
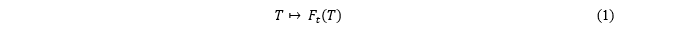

The shape of the futures curve is important to commodity hedgers and speculators. Both care about whether commodity futures markets are in contango or in backwardation. Contango and backwardation refer to the pattern of futures prices over time, specifically if the price of the contract is rising or falling. However, a mixed behavior is also possible. For instance, in February 2020 crude oil futures curve is humped: it is rising in the short-term but gives way to a decrease in prices for longer maturities. Switching between contango and backwardation is linked to a change in view of market participants on fundamentals like storage cost, funding costs, and convenience yield. Contango may be usual in markets with a cost of carry greater than the convenience yield. For example, agricultural markets show both the shapes in February 2020: coffee and soybeans are in backwardation, while cocoa and sugar are in contango.
More complex patterns may also arise in the term structure of commodity futures prices. Many commodities show a strong seasonality, for instance, there is more natural gas demand (for heating) in winter than in summer. Seasonality patterns may change in time, in particular if they are linked to physical phenomena as for agricultural. Moreover, patterns on different time scales may emerge as in the electrical market since the power consumption has a characteristic pattern over the day, the week, and the year.
Market quotes as the maturity date increases become sparser and the corresponding futures contracts may be quoted only on few delivery periods. In the case of TTF futures contracts we have quotes for contracts over delivery periods of one, three, six months and one year only for short maturities, and shorter periods are no longer quoted for longer maturities. Our goal is to introduce an interpolating scheme for the term structure with shortest delivery period and to deduce from it the term structures of longer delivery periods. The interpolation scheme must be able to avoid arbitrages between contracts with different delivery periods and to accurately describe the complex patterns of the term structure present in the market.
3 Interpolating noisy data with Kriging
If we wish to build a complete term structure for futures prices, we need (i) to model different shapes (backwardation, contango, mixed), (ii) to deal with seasonalities (possibly on different time scales), (iii) to weight bid-ask spreads, (iv) to bootstrap quotes from the prices of overlapping linear products.
In the following, we consider Kriging, a Bayesian approach, to include all this features. The basic idea of Kriging is to predict the value of an unknown function at a given point by computing a weighted average of the known values of the function in the neighborhood of the point. Originally, developed for geophysical problem by (Krige, 1951) and (Matheron, 1963), this technique is also known as Gaussian process regression, or Wiener-Kolmogorov prediction. We wish to use Kriging as an effective interpolating technique for the futures term structure.


4 Numerical examples with TTF natural gas
We consider the futures and futures-spread contracts observed on 14 January 2020 on ICE market for TTF natural gas. We have bid-ask quotes for
- futures contracts with a delivery period of one month up to June 2020;
- futures contracts with a delivery period of three months up to the first quarter 2021;
- futures contracts with a delivery period of six months up to the summer 2022;
- futures contracts with a delivery period of one year up to 2023;
- futures-spread contracts with a delivery period of one month and three months for some maturities.
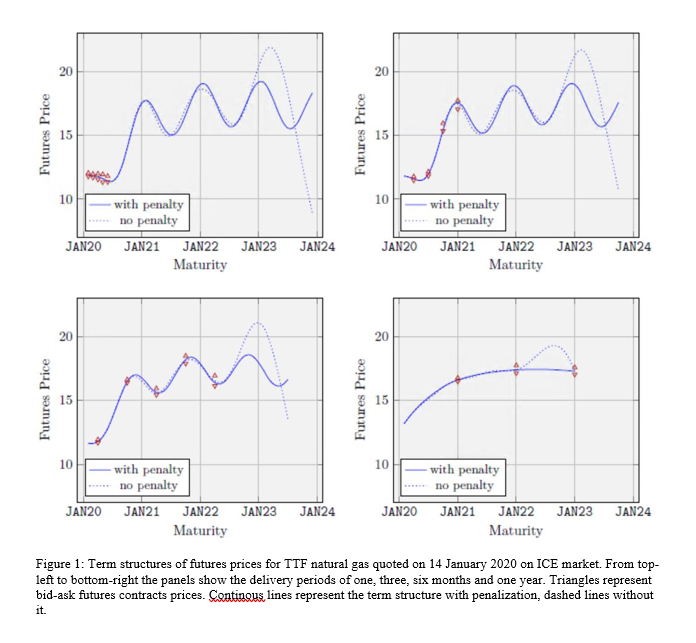
In the following, we model them all along with a penalization for seasonality effects. In Figure 1 we show the market bid-ask quotes along with the resulting term structures for the four delivery periods of one, three, six months and one year. The continuous lines represent the term structures with the penalization to include seasonality effects, while the dashed lines represent the term structure without the penalization, so that we can appreciate the impact of the penalizing term. We can see that Kriging with the penalization term is able to fit well all market data.
[1] The term-sheet and quotes of futures contracts on TTF natural gas can be found on ICE exchange at https://www.theice.com/products/27996665/Dutch-TTF-Gas-Futures.



