How Digital transformation is transforming CFOs agenda
Digital Transformation in the Financial Services is changing the way how business operates leveraging on new technologies and processes to create—and to sustain—a competitive advantage, byimproving efficiency, empowering new products and services, enabling new business models to overcome the boundaries among industries.

Looking at the Finance area, the Digital Transformation is being started to re-think and support the core processes and to introduce new innovative ones, as emerging from the CFOs agenda[1]:
- Finance success will be related to a combination of humans, robots and algorithms, as stated by over 42% of CFOs, implying the need for new processes definition impacting the way Business is supported in the Decision-Making process;
- New technologies, such as Artificial Intelligence, will represent a distinctive factor to raise the bar of prediction and accuracy – over 60% of Finance Leaders say that using data science and leveraging on power of advanced analytics is a top influence on their strategy for delivering accurate financial reports to support/ anticipate business decisions;
- The time dedicated to traditional activities in favour of strategic and highly innovative activities is decreasing[2], expecting a shift from standard reporting/ analysis to cognitive/ predictive analysis.
Several constraints for Finance growth are internal (organization structure, siloed behaviors, culture, inefficiency, etc.), as 80% of CFOs are declaring, leading to the identification of new interventions to change their organizational model supported by the new technologies
The focus highlighted by Finance Leaders on actuals and predictions accuracy to proactively support the business Decision-Making process leveraging on Big Data and AI has a specific impact on “Planning & Control” transformation and streamlining journey.
How Planning & Control is going to rethink the support to Decision-Making
Within the CFO area, Planning and Control function is preparing for its own streamlining, boosted by the digital transformation
1.Roles & Operating Model, P&C as a new Business Partner
The application of Automation, Robotics and AI will allow Planning & Control functions to re-interpret and reinforce the “proactive partnering” role, providing Business people (Relationship Managers, Sales, Traders etc…) with “just in time” data, new insights, advanced visualization and storytelling – moving from the “cut and paste” era, spending time to crunch and reconcile figures, to “advanced financial analyses” one, granting continuing osmosis with commercial and business areas.
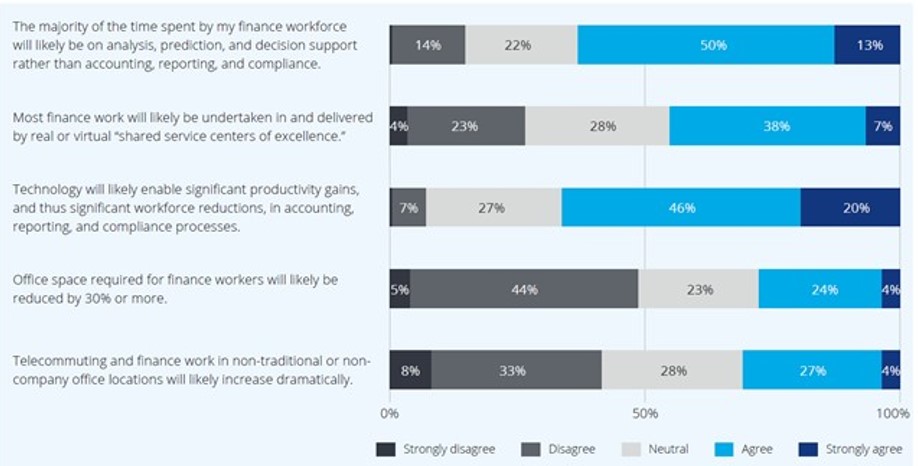
“What does this tell me about the business?” and “How can the business close gaps in performance expectations?” will be the future key questions, requiring for a strong business centric service, dedicated new skills and new organizational structures:
- Business centric operating model will lead to new agile pool of resources with differentiated service levels for the different business stakeholders (e.g. co-location, co-processes and new technological solutions will be key to grant business and P&C people constantly connected)
- Cross-functional teams leveraging on differentiated but integrated competences will include not only business experts, but also “Finance Data scientist” (statistical and mathematical models skills), “Finance Data engineer” (data preparation and visualization skills) together with story-tellers and cognitive psychologists
- Contamination between Business traditional specific roles and the “Data Science” will be key to unlock the potential and to enable the creation of value stemming from the (Big) Data and AI
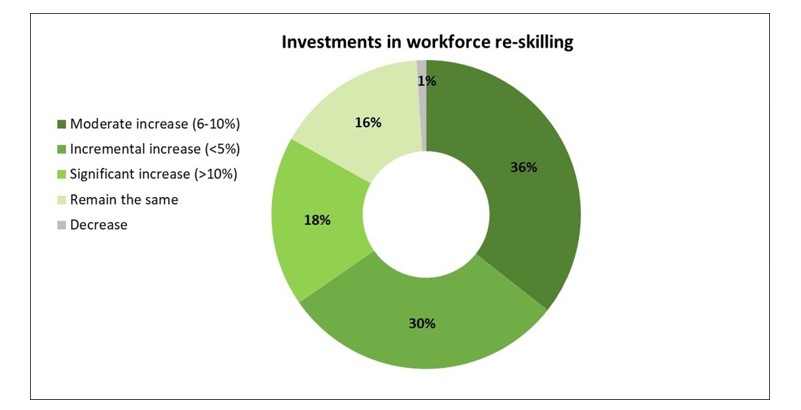
- This network of teams will not be able to be ready in the near future if a dedicated “re-skilling” program won’t take place supported by the Talent function
- New “orga charts” will come up in the next years, where Planning and Control function will continue to be a key role for the CFO, but as some players are already experiencing, “hub & spoke” models will take place to leverage on one hand on a central strong governance, and on the other hand with the possibility to have effective peripheral impact with business departments (e.g. Corporate)
2. Planning & Control cycle revolution
The standard “Planning & Control” cycle, where periodic phases are envisaged with e.g. monthly and quarterly cadence, is less and less consistent with the new digital bank business models, where everything happens quickly and the Decision Making process is always more a “matter of seconds”.
Following this new approach, Planning & control function will no longer “simply” plan the business and control the results, but supported by the new AI/tech solutions will play a more business integrated role . This will be much more inclusive and close to the business, where the cooperation will be granted on a daily/ “on demand” basis and not only during the periodic close.
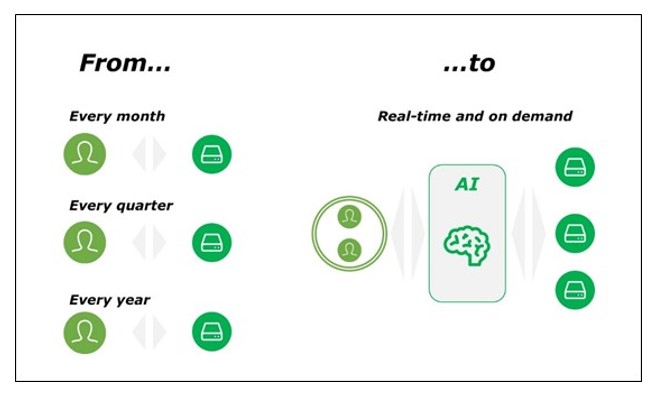
For this reason, an evolution of this standard cycle seems to be not only useful, but also a key survival factor to be able to answer and support business people. This will lead to a paradigm overturning from the pure “Planning and Control” to the future “Foreseeing, Oversight and Advice”:
- Foreseeing, to predict future market trends and create competitive advantage through, for example, advanced analytics and machine learning solutions applied to apparently unrelated features;
- Oversight, to achieve streamlined and automated supervision on performance management controlling through the adoption of AI techniques with a wider scope and a data science driven view (e.g. machine learning on selected features, performance monitoring on algorithms output);
- Advice, to closely and actively support the top management and commercial network in decision making through artificial intelligence methodologies which provide augmented awareness of data through deeper insights and hidden patterns, amplifying human capabilities. As a result, humans are able to enrich these insights with their unpaired feel and understanding of the business.
These three elements are structurally interrelated and imply a new processes and operating framework definition: leaving behind operative tasks which will be replaced by robots and algorithms, people will do more human work including exception based and insight driven activities.
In addition to internal pros, real-time and self-service access to data has another positive outcome on the capability to provide fast response to the increasing demand of information from external stakeholders (e.g. regulators, investors), leading to a progressive convergence between internal and external needs.
3. Data, models and functions: the ingredients of Innovation
The automation and AI represents for the Finance Area, and specifically for Planning & Control, a key transformation opportunity which will affect all the core traditional processes, granting more efficiency, but also the innovative ones to bring new insights, real time suggestions, etc.
The automation and AI represents for the Finance Area, and specifically for Planning & Control, a key transformation opportunity which will affect all the core traditional processes, granting more efficiency, but also the innovative ones to bring new insights, real time suggestions, etc.
Data feeding, elaboration and reporting are going to be revised to benefit from the new technologies:
- Data feeding volume, variety and velocity will be supported by new architectures, mixing both traditional relational models with big data one, including new and unstructured data which can be more easily integrated and used to support business analysis (e.g. relationship manager, network default contagion for risk evaluations, etc.)
- Data elaboration and models will be strongly improved both in terms of:
- “process timing” which allows to increase the efficiency and reduce the effort of human interventions (e.g. cognitive solution to automatically perform data forecasting on past figures)
- “data enhancement/ augmentation”, which allows to generate new figures and insight, leveraging on advanced data science algorithms (e.g. predictive forecasting solution, aimed at predicting the financial future of Business thanks to algorithm able to “learn” from previous cycles, passing from “pure planning” to “foreseeing and oversight”) – Artificial Intelligence is a relevant mean to reduce cognitive bias coming from human behavior[3], therefore these solutions will transform the capability supporting the “decision making process”.
- Data reporting will no longer be prepared/ integrated manually via human activities. However, it won’t just be a matter of full automation only to increase the efficiency, but it will be revised to offer a new user experience boosting the process. For example, the application of Deep Learning-NLP solutions will enhance reporting experience, leveraging on linguistic rules to both navigate data and reports and for “instant commenting” via language rules which mimic business speech. This will be a significant contribution to pass form pure profitability results monitoring to a proactive advice, where business support is boosted with less risk of cognitive bias.
An applied case of transformation leveraging on AIAn applied case of transformation leveraging on AI
The banking ecosystem is actively responding to the transformation strengths with dedicated strategies to evolve. Many distinctive characteristics of such evolution can be observed on one of the largest European banking groups where AI and its applications are one of the main pillar of the multi-year industrial plan. In this case the Group is moving on two drivers adopting a two-speed roadmap:
- On one side, it is rapidly implementing AI best practices in the Finance area where main applications are seen in performance management processes. Predictive models and cognitive solutions have created discontinuity on the traditional way of thinking and working. For example, in forecasting processes, predictive intelligence algorithms have been adopted to enhance profitability engines, which now provide:
- Increased accuracy of profitability estimate through regression trees and ARIMA model for time series forecasting
- Reduced number of manual corrections made by the controllers and optimized processes.
- Single-client profitability to drive capital allocation adjustments through classification trees and K-means algorithm for client clustering
- On the other side, the Group is deeply committed on a long term transformation path of its workforce and organization; the Group has put in place relevant investments to re-skill its workforce through highly specialized training programs (e.g. for the Finance Data Scientist). As a direct consequence, the Group is also re-designing its organization to have AI coverage on as many areas as possible, thus making it a strategic asset to support transformation.
Along with these new challenges, the Group has also set up a strategy to fill the gap in areas of improvement which represent a key success factor for the “AI value chain” to work correctly:
- Upstream, data need to meet high quality standards to allow AI to generate significant insights; source redundancy has to make room for single point of truth; as of today, P&C and, in general, Finance IT systems are still affected by some silos causing partial synergies with other areas, Risk for instance
- Downstream, processes and analysis are still partially biased by a mindset oriented to traditional P&C cycles. Reporting processes are still tied to periodicity and clearance/ reconciliation purposes reducing the possibility of being an enabling factor to achieve ongoing strategic decision making support and business partnership.
Despite the Group has moved its beginning steps into this transformation journey, the Finance area has started acknowledging the added value that first AI applications are delivering.
What’s next
Finance leaders are going to investigate and consolidate the answers to the strategic questions to effectively manage the Digital Transformation, increasing the awareness on how AI solutions, which are growing exponentially, can support the Decision-Making.
While operational finance will be potentially leaner in the near future thanks to automation and robotics solution, the expectations for support from Business Finance to the Decision-Making (Business partnering, reporting, budgeting, forecasting, ….) will continue to grow.
The timing and the characteristics of this grow will depend on both the internal maturity/ awareness of the Finance area and new technologies reliability which will lead to different paths of evolution, from cherry-picked process redesign to advanced finance models evolution, wide people re-skilling and technology scale-up to effectively be business partners achieving synergies among the organization’s functions.
Autori:
Luigi Mastrangelo – Partner, DCM Finance & Performance Offering Leader
Davide Grassi – Director, Deloitte Consulting
Rosario Laface – Senior Manager, Deloitte Consulting
Michele Angarano – Manager, Deloitte Consulting
Alice Cortese – Consultant, Deloitte Consulting
[1] CFO Forums, CFO Transition LabTM, Deloitte Dbrief webcast
Deloitte Survey – Gfk Eurisko, Harvard Business Review
Deloitte survey 2019 – CFO Program’s – Transition Lab
[2] Deloitte – Crunch Time. CFO talks
[3] D. Kanheman, Thinking, Fast and Slow, Farrar, Straus and Giroux, 2011