The European Securities and Markets Authority (ESMA) has updated today its public register with the latest set of double volume cap (DVC) data under the Markets in Financial Instruments Directive (MiFID II)…

L’iniziativa di Finriskalert.it “Il termometro dei mercati finanziari” vuole presentare un indicatore settimanale sul grado di turbolenza/tensione dei mercati finanziari, con particolare attenzione all’Italia.
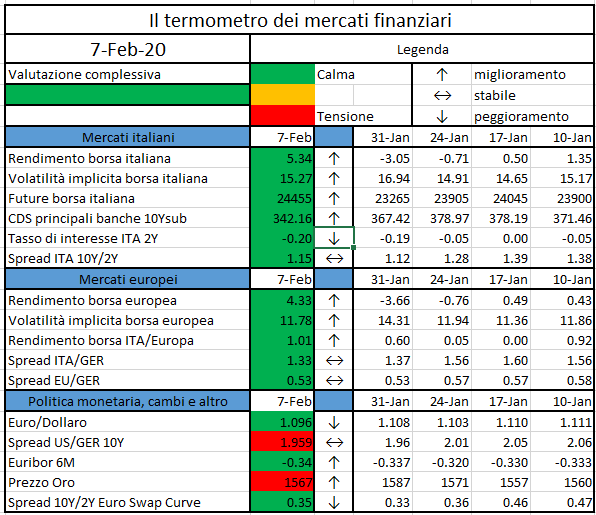
Significato degli indicatori
- Rendimento borsa italiana: rendimento settimanale dell’indice della borsa italiana FTSEMIB;
- Volatilità implicita borsa italiana: volatilità implicita calcolata considerando le opzioni at-the-money sul FTSEMIB a 3 mesi;
- Future borsa italiana: valore del future sul FTSEMIB;
- CDS principali banche 10Ysub: CDS medio delle obbligazioni subordinate a 10 anni delle principali banche italiane (Unicredit, Intesa San Paolo, MPS, Banco BPM);
- Tasso di interesse ITA 2Y: tasso di interesse costruito sulla curva dei BTP con scadenza a due anni;
- Spread ITA 10Y/2Y : differenza del tasso di interesse dei BTP a 10 anni e a 2 anni;
- Rendimento borsa europea: rendimento settimanale dell’indice delle borse europee Eurostoxx;
- Volatilità implicita borsa europea: volatilità implicita calcolata sulle opzioni at-the-money sull’indice Eurostoxx a scadenza 3 mesi;
- Rendimento borsa ITA/Europa: differenza tra il rendimento settimanale della borsa italiana e quello delle borse europee, calcolato sugli indici FTSEMIB e Eurostoxx;
- Spread ITA/GER: differenza tra i tassi di interesse italiani e tedeschi a 10 anni;
- Spread EU/GER: differenza media tra i tassi di interesse dei principali paesi europei (Francia, Belgio, Spagna, Italia, Olanda) e quelli tedeschi a 10 anni;
- Euro/dollaro: tasso di cambio euro/dollaro;
- Spread US/GER 10Y: spread tra i tassi di interesse degli Stati Uniti e quelli tedeschi con scadenza 10 anni;
- Prezzo Oro: quotazione dell’oro (in USD)
- Spread 10Y/2Y Euro Swap Curve: differenza del tasso della curva EURO ZONE IRS 3M a 10Y e 2Y;
- Euribor 6M: tasso euribor a 6 mesi.
I colori sono assegnati in un’ottica VaR: se il valore riportato è superiore (inferiore) al quantile al 15%, il colore utilizzato è l’arancione. Se il valore riportato è superiore (inferiore) al quantile al 5% il colore utilizzato è il rosso. La banda (verso l’alto o verso il basso) viene selezionata, a seconda dell’indicatore, nella direzione dell’instabilità del mercato. I quantili vengono ricostruiti prendendo la serie storica di un anno di osservazioni: ad esempio, un valore in una casella rossa significa che appartiene al 5% dei valori meno positivi riscontrati nell’ultimo anno. Per le prime tre voci della sezione “Politica Monetaria”, le bande per definire il colore sono simmetriche (valori in positivo e in negativo). I dati riportati provengono dal database Thomson Reuters. Infine, la tendenza mostra la dinamica in atto e viene rappresentata dalle frecce: ↑,↓, ↔ indicano rispettivamente miglioramento, peggioramento, stabilità rispetto alla rilevazione precedente.
Disclaimer: Le informazioni contenute in questa pagina sono esclusivamente a scopo informativo e per uso personale. Le informazioni possono essere modificate da finriskalert.it in qualsiasi momento e senza preavviso. Finriskalert.it non può fornire alcuna garanzia in merito all’affidabilità, completezza, esattezza ed attualità dei dati riportati e, pertanto, non assume alcuna responsabilità per qualsiasi danno legato all’uso, proprio o improprio delle informazioni contenute in questa pagina. I contenuti presenti in questa pagina non devono in alcun modo essere intesi come consigli finanziari, economici, giuridici, fiscali o di altra natura e nessuna decisione d’investimento o qualsiasi altra decisione deve essere presa unicamente sulla base di questi dati.
The European Securities and Markets Authority (ESMA) has published seven opinions on position limits regarding commodity derivatives under the Markets in Financial Instruments Directive and Regulation (MiFID II/MIFIR) today…
https://www.esma.europa.eu/press-news/esma-news/esma-issues-opinions-position-limits-under-mifid-ii
The parent company behind the bitcoin-based smart contract platform RSK has launched a new token bridge joining it to ethereum…
https://www.coindesk.com/rsk-launches-interoperability-bridge-between-bitcoin-and-ethereum
Speech by Ms Lael Brainard, Member of the Board of Governors of the Federal Reserve System, at the Symposium on the Future of Payments, Stanford, California, 5 February 2020…
La Banca Centrale europea ha posto in pubblica consultazione la guida che delinea la metodologia utilizzata dalla BCE per valutare i modelli interni…4
ABSTRACT: Anche se le funzioni di risk management nelle banche e la normativa di riferimento sono in una fase che possiamo definire matura del loro sviluppo, non si può affermare che questo ambito sia cristallizzato e risolto in modo del tutto soddisfacente. Lo testimonia la continua e sempre più frequente aggiornamento delle normative. Nel paper, senza pretesa di esaustività, una sintesi comparativa con alcuni spunti di riflessione.
1 La ricerca del rischio e l’evoluzione del framework “Basilea”
Molti termini nel linguagggio comune sono usati (talvolta usabili) in modo sovrapposto, con varie declinazioni dal linguaggio comune e quello tecnico e varie evoluzioni nel tempo: sorte, alea, incertezza, rischio, pericolo.
E come sottolinea brillantemente Ivar Ekelend nel suo saggio del 1987 “A Caso” (cfr [13]), il confine tra il caso, la causa determinsitica, il caos, è spesso indefinito, legato a percezioni soggettive e più ampie evoluzioni culturali.
Perché il gioco dei dadi è ritenuto un gioco d’azzardo, di sola alea, mentre il gioco del biliardo è uno sport?
La traiettoria e la posizione di arresto di un dado, così come per una palla da biliardo, sono perfettamente determinate dalle leggi della meccanica. Leggi non facili perché bisogna tenere conto anche di aspetti fenomenologici specifici come il materiale su cui si gioca e conseguente attrito, radente o viscoso, ma pur sempre leggi perfettamente note.
In fondo, è più difficile gettare il dado in modo che esca il “6” dopo i rimbalzi o colpire nel biliardo in modo da mettere la palla in buca dopo 7 carambole sulle sponde del tavolo? Forse la forma sferica contro quella con spigoli alternao il nostro giudizio.
E in fondo, pensando che i giocatori di dadi prendano una piccola rincorsa prima del lancio, in cosa il lancio d’azzardo del dado è diverso dal gioco (sport) delle bocce? A un approccio oggettivo e rigoroso, si capisce come entrambe le atttività non abbiano gradi così diversi di alea, o quantomeno debbano essere qualificati in una stessa omogenea categoria, per esempio “gioco di abilità”.
Perché questa premessa? Per motivare come sia di difficile o forse impossibile una definizione in qualche modo assoluta di termini come incertezza, rischio. E quindi come sia ancora più sfidante il tentativo di quantificare il rischio, di ottenere cioè una utile misura, o stima, dello stesso.
La regulation bancaria, sin dal primo accordo di Basilea del 1988, ha come caposaldo la necessità per le banche di un capitale adeguato rispetto ai rischi. Quindi la misura di tali rischi è elemento essenziale della ratio normativa.
Negli anni fino all’accordo di Basilea 3, divenuto efficace nel 2014 ([14]), le autohorities hanno spinto verso l’adozione dei modelli interni, cioè modelli statistici di misura dei rischi sviluppati dalle banche stesse, ovviamente all’interno del framework (quali misure di rischio, vincoli di qualità del modello o sui parametri) normativo.
Al contrario, all’interno del complesso corpo normativo noto come Basilea 4, che in estrema sintesi sarà in vigore da inizio 2022, lo stesso comitato di Basilea è andato nella direzione opposta, cioè rimozione o sempre maggiori vincoli sui modelli interni, in favore di nuove versioni dei modelli standard. Modelli cioè in cui l’algoritmo di calcolo della misura dei rischi e relativi parametri e pesi sono totalmente prescritti nella normativa.
Queste nuove versioni si caratterizzano per una marcata maggiore complessità rispetto ai modelli standard correnti, con l’ambizione di essere più risk sensitive, accurati quindi nella capacità di rappresentare i fattori di rischio. Nelle prossime sezioni cercheremo di dare una review di tali evoluzioni, con alcune riflessioni finali.
2 I nuovi modelli standard
2.1 Le innovazioni
Già partire dal 2013, quando Basilea 3 era ai suoi primi passi, sono inziati tramite vari gruppi di lavoro attività di ulteriore revisione e finalizzazione dei modelli. Va qui ricordato che se ci soffermiamo sulla componente core del framework di Basilea, non sull’introduzione dei nuovi vincoli di liquidità, l’unico elemento realmente nuovo di discontinuità in Basilea 3 è stato l’introduzione di un nuovo requisito di capitale, il noto CVA capital charge, cioè il rischio di perdite inattese dovute al deterioramento del merito di credito delle controparti di posizioni in derivati OTC.
Tutte le ulteriori finalizzazioni successive, in un primo tempo spesso citate come “Basilea 4”, sono state raccolte in un tentativo di corpo unico, si veda [2].
Vediamo la lista completa degli interventi previsti:
- Rischio Operativo. Rimozione dei modelli interni (AMA), in favore di un unico apprccio standardizzato (SMA), si veda [15]
- Rischio di Credito e
Controparte
- rimozione dei modelli interni per controparti finanziarie e large corporate
- evoluzione dei modelli standard ([11]).
- vincoli sui parametri e misure di RWA dei modelli interni IRB ([12])
- nuovo modello standard calcolo esposizione (EAD) su derivati, detto SA-CCR, si veda [6], [7].
- Rischio di mercato.
Totale revisione con la riforma FRTB (cfr. [3], [4] e [5]), in breve:
- Modelli interni. Passaggio da misure di tipo VaR a misure di Expercted Shortfall per capital charge
- Evoluzione delle procedure di backtesting e introduzione di ulteriore test di qualità del modello, noto come PLA (P&L Attribution)
- significativa evoluzione dei modelli standard (SBA, sensitvity based approach)
- CVA capital charge. Abbandono del modello interno in favore di un nuovo modello standard, si veda [8], [9], [16]
2.2 Il razionale comune dei nuovo modelli standard
Motivi di spazio non consentono una disanima comparativa di tutti i “nuovi” modelli standard, ma ci sofferiamo su alcuni di essi per le caratteristiche comuni che li caraterizzano e alcune considerazioni che possiamo trarne. In particolare ci focalizziamo su:
- rischio di mercato, cioè rischio di perdite derivanti da variazioni inattese negative del valore (mark to market)
- rischio di controparte, inteso come rischio di crescita inattesa delle esposizioni (EAD) sui derivati OTC, dovute in questo caso a variazioni positive del mark to market
- CVA risk, dovuto alla posibilità di perdite inattese (unrealized, però registrate in conto economico) per variazioni improvvise del CVA “contabile”, cioè della rettifica del MtM legata al merito di credito delle controparti.
Si può dire che per la loro natura la genesi dei rischi è la stessa, cioè il MtM e le sue variazioni.
Vediamo le interessanti analogie (con qualche distinguo che omettiamo per brevità) in relazione alla misura dei rischi:
- Tassonomie e Fattori di rischio. Per tutti questi rischi è specificata una tassonomia dei fattori di rischio molto più granulare che per i modelli standard correnti, che si può riassumere nella seguente gerarchia partendo dall’alto: A) Risk types B) buckets o hedging sets C) Tenors D) fattore di rischio elementare. Risk types è riferito alla asset classe, quindi tassi di interesse, tassi di cambio, equity, commodity, posizioni di credito. Il bucket/heding set può essere come nel caso delle posizioni in tassi di interesse dato da ciascuna currency, per equity vi può essere un unico bucket o più bucket in base a geografia, settore, size, le commodity sono scomposte in gruppi omogenei, per i tassi di cambio ogni currency costituisce un bucket. I tenors, cioè le scadenze, sono significative solo per le posizioni in tassi di interesse. Infine abbiamo i fattori di rischio elementari. Si ribadisce che questo dettaglio sui fattori di rischio da identificare e mappare è molto più elevato che in precedenza.
- Struttura del requisito di capitale e aggregazione tra posizioni. Anche qui significative novità, nel senso che la gerarchia anarafica vista prima ha lo scopo di gestire correlazioni tra fattori di rischio o tra gruppi di essi prima non previsti. Più in generale 1) sono fornite matrici di correlazione tra fattori di rischio all’interno del bucket 2) sono fornite matrici di correlazione tra buckets all’interno di una asset class 3) per market risk e cva risk si usano matrici di correlazione in 3 scenari per tenere conto di possibile stress. Lo “step zero” del calcolo è la determinazione per ogni posizione della sensitivity (per market risk e cva capital charge) o di esposizione (per counterparty risk), su cui si applicano i risk weight e si procede poi con le aggregazioni mediante matric di correlazione sopra dette.
Mostriamo a titolo esemplificativo alcuni parametri riferiti alla asset class azionaria, in cui abbiamo un bucket per ogni emittente:
- Market risk FRTB. Il fattore di rischio è dato da ogni single name o indice. I bucket sono 12 per cluster di settore, dimensione, geografia. Il risk weight applicato varia da un minimo del 15% per indici di mercati evoluti al 70% di azioni small cap dei mercati emergenti. Le correlazioni nel bucket e tra bucket assumono valori molto diversificati (mai comunque negativi) in relazione ai casi, per esempio 15% tra due azioni large cap dei mercati europei, 80% tra due indici di mercati europei.
- Rischio di controparte. Per determinare l’add-on rispetto al mark to market, da cui discende l’esposizione soggetta a rischio, si hanno due risk weights: 32% per le azioni e 20% per gli indici, con correlazione del 50% tra azioni e 80% tra indici.
- CVA Risk. I bucket come nel rischio di mercato, anche se non è previsto un CVA risk azionario per posizioni su indici. Risk weights tra 35% e 70%. Correlazioni tra bucket pari al 15%.
Riproduciamo anche il contributo al requisito di capitale per ogni bucket Kb e la sua aggregazione per ogni asset class
Market risk FRTB

Si può notare come, al netto di lievi differenze di notazione, tutte le formle in qualche modo mimano la volatilità di un portafoglio ben nota dalle teorie dell’asset allocation e del modello CAPM. Anzi, a essere più precisi, il senso di queste formule è quello di un VaR, cioè un percentile, sulle grandezze soggette a rischio (perdite di mark to market, espansioni di mark to market, incrementi di CVA), in quanto i risk wieght usati come mattone di base sono calibrati su eventi estremi. Se riprendiamo i dati sopra forniti e tenendo conto che l’orizzonte tradizionale per il market risk è 10 giorni lavorativi, un risk weight del 15% per posizioni su indici implica considerare questa come possibile perdita estrema di un indice di mercati evoluti, scenario molto prudente, in linea con gli obiettivi di Basilea, e non certo la sua normale volatilità.
3 Alcune riflessioni
Modelli interni in fase di estinzione, modelli standard sempre più evoluti verso un approcio di portafoglio che era prerogativa dei modelli interni, con la complessa algebra delle matrici a supporto, e molto dettagliata definizione delle tassonomie. Possiamo dare un giusdizio su questo trend, molto significativo e irreversibile? E’ un fallimento del risk management bancario dopo che Basilea 2 aveva al contrario introdotto i modelli interni sul rischio di credito e sui rischi operativi?
Nel framework di Basilea 2 vi erano già dei “puntelli” ai gradi di libertà dei modelli interni. Uno ovvio, cioè la richiesta di documentare in modo formale la capacità predittiva dei modelli di misura del rischio tramite tecniche di baktesting specifiche per i vari tipi di rischio. Il secondo e più interessante puntello è costituito dal fatto che per i modelli sul rischio di credito le banche possono limitarsi ad avere modelli di stima dei parametri (PD,LGD,EAD), mentre per il calcolo del capital charge devono applicare la formula prevista per i modelli IRB, a differenza del rischio di mercato e operativo dove anche il modello di perdita, dati i fattori di rischio, è costruito dalla banca.
Non è bastato. Troppi i margini di discrezionalità e le difficoltà di omogeneizzazione nei rischi operativi, eccessivo l’uso di modelli “aggressivi” per minimizzare il capitale richiesto, sui modelli per la PD e (soprattutto) LGD, come dimostrato in vari benchmarking internazionali.
Ma la strada intrapresa è corretta? A giudizio di chi scrive sì, con tutte le possibili migliorie nel tempo. Da un lato finalmente anche banche medie o medio piccole applicheranno metodi più risk sensitive con una maggiore consapevolezza del legame tra rischi e buffer di capitale. Dall’altro, in queste stesse banche ma anche in quelle maggiori finalmente la struttura di Risk Management potrà diventare in modo più incisivo owner del processo segnaletico di I pilastro, che è oggi tradizionalmente allocato nelle banche nella “Direzione Amministrazione”, dove però, specialmente sui rischi di mercato, difficilmente vi sono competenze sufficienti per il controllo delle misure finali. Infine nulla impedirà alle banche, in ambito di II pilastro e processi RAF, di continare a utilizzare modelli interni più sofisticati, se confidenti sulle loro performance e se questi sono realmente utilizzati nei processi gestionali di delega e controllo dei rischi.
Riferimenti
[1] Basel Committee on Banking Supervision (2011), “Basel III: A global regulatory framework for more resilient banks and banking systems – revised version June 2011”
[2] Basel Committee on Banking Supervision (2017), “Basel III: Finalising post-crisis reforms”
[3] Basel Committee on Banking Supervision (2019), “Minimum capital requirements for market risk”, paper 457.
[4] Basel Committee on Banking Supervision (2017), “Simplified alternative to the standardised approach to market risk capital requirements”, paper 408.
[5] Basel Committee on Banking Supervision (2014), “Fundamental review of the trading book: outstanding issues”, paper 305.
[6] Basel Committee on Banking Supervision (2014), “The standardised approach for measuring counterparty credit risk exposures”, paper
[7] Palombini E. Zottarel M. (2016) Il nuovo Standardised Approach for Counterparty Credit Risk (SA-CCR)
[8] Basel Committee on Banking Supervision (2015), “Review of the Credit Valuation Adjustment Risk Framework “, paper 325.
[9] Axis Alternative (2019), “New CVA capital framework: FRTB-CV”.
[10] ISDA (2019), “ISDA SIMMTM,1 Methodology, version 2.2 “.
[11] Basel Committee on Banking Supervision (2015), “Revisions to the Standardised Approach for credit risk“.
[12] Basel Committee on Banking Supervision (2016), “Reducing variation in credit risk-weighted assets – constraints on the use of internal model approaches”.
[13] Ekeland I.(1987), A Caso (Mathematics and the Unexpected), Bollati Boringhieri
[14] EU (2013), “Capital Requirement Regulation (CRR)”, Regulation 575/2013 (Basilea 3).
[15] Basel Committee on Banking Supervision (2016), “Standardised Measurement Approach for operational risk”
[16] Basel Committee on Banking Supervision (2019), “Credit Valuation Adjustment risk: targeted final revisions”, consultation paper.

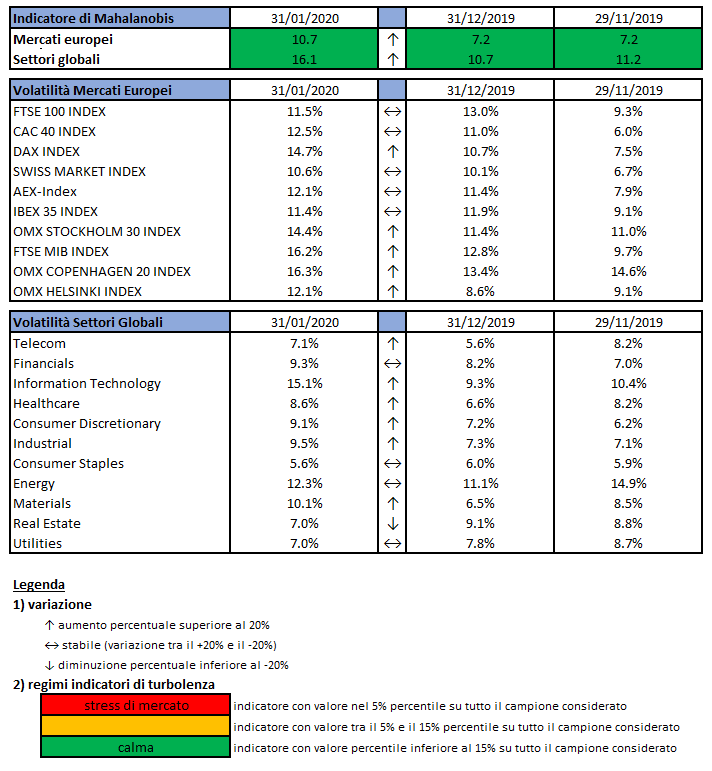
L’indicatore di Mahalanobis permette di evidenziare periodi di stress nei mercati finanziari. Si tratta di un indicatore che dipende dalle volatilità e dalle correlazioni di un particolare universo investimenti preso ad esame. Nello specifico ci siamo occupati dei mercati azionari europei e dei settori azionari globali.
Gli indici utilizzati sono:
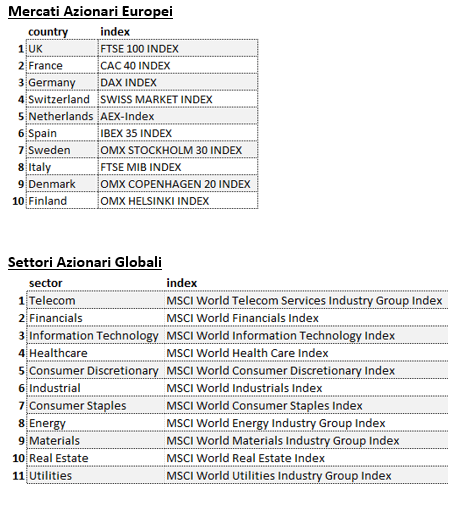
Le volatilità riportate sono storiche e calcolate sugli ultimi 30 trading days disponibili. Per ogni asset-class dunque sono prima calcolati i rendimenti logaritmici dei prezzi degli indici di riferimento, successivamente si procede col calcolo della deviazione standard dei rendimenti, ed infine si procede a moltiplicare la deviazione standard per il fattore di annualizzazione.
Per il calcolo della distanza di Mahalnobis si procede dapprima con la stima della matrice di covarianza tra le asset-class. Si considera l’approccio delle finestre mobili. Come con la volatilità, si procede prima con il calcolo dei rendimenti logaritmici e poi con la stima storica della matrice di covarianza, come riportato di seguito.
Supponendo una finestra mobile di T periodi, viene calcolato il valore medio e la matrice varianza covarianza al tempo t come segue:

La distanza di Mahalanobis è definita formalmente come:

Le parametrizzazioni che sono state scelte sono:
- Rilevazioni mensili
- Tempo T della finestra mobile pari a 5 anni (60 osservazioni mensili)
Le statistiche percentili sono state calcolate a partire dalla distribuzione dell’indicatore di Mahalanobis dal Dicembre 1997 al Dicembre 2019 su rilevazioni mensili.
Ulteriori dettagli sono riportati in questo articolo.
Disclaimer: Le informazioni contenute in questa pagina sono esclusivamente a scopo informativo e per uso personale. Le informazioni possono essere modificate da finriskalert.it in qualsiasi momento e senza preavviso. Finriskalert.it non può fornire alcuna garanzia in merito all’affidabilità, completezza, esattezza ed attualità dei dati riportati e, pertanto, non assume alcuna responsabilità per qualsiasi danno legato all’uso, proprio o improprio delle informazioni contenute in questa pagina. I contenuti presenti in questa pagina non devono in alcun modo essere intesi come consigli finanziari, economici, giuridici, fiscali o di altra natura e nessuna decisione d’investimento o qualsiasi altra decisione deve essere presa unicamente sulla base di questi dati.

L’iniziativa di Finriskalert.it “Il termometro dei mercati finanziari” vuole presentare un indicatore settimanale sul grado di turbolenza/tensione dei mercati finanziari, con particolare attenzione all’Italia.
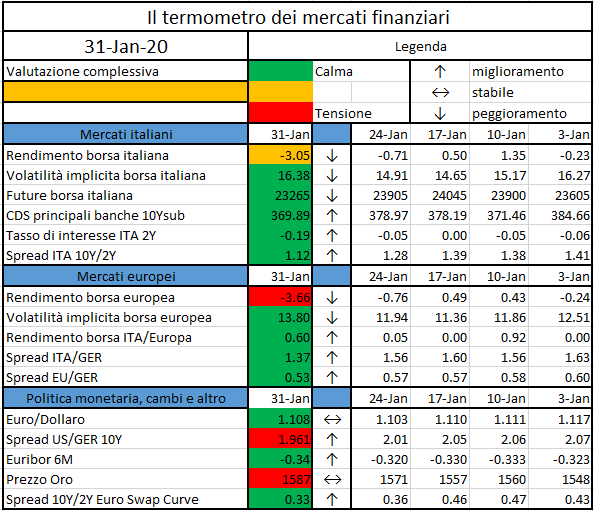
Significato degli indicatori
- Rendimento borsa italiana: rendimento settimanale dell’indice della borsa italiana FTSEMIB;
- Volatilità implicita borsa italiana: volatilità implicita calcolata considerando le opzioni at-the-money sul FTSEMIB a 3 mesi;
- Future borsa italiana: valore del future sul FTSEMIB;
- CDS principali banche 10Ysub: CDS medio delle obbligazioni subordinate a 10 anni delle principali banche italiane (Unicredit, Intesa San Paolo, MPS, Banco BPM);
- Tasso di interesse ITA 2Y: tasso di interesse costruito sulla curva dei BTP con scadenza a due anni;
- Spread ITA 10Y/2Y : differenza del tasso di interesse dei BTP a 10 anni e a 2 anni;
- Rendimento borsa europea: rendimento settimanale dell’indice delle borse europee Eurostoxx;
- Volatilità implicita borsa europea: volatilità implicita calcolata sulle opzioni at-the-money sull’indice Eurostoxx a scadenza 3 mesi;
- Rendimento borsa ITA/Europa: differenza tra il rendimento settimanale della borsa italiana e quello delle borse europee, calcolato sugli indici FTSEMIB e Eurostoxx;
- Spread ITA/GER: differenza tra i tassi di interesse italiani e tedeschi a 10 anni;
- Spread EU/GER: differenza media tra i tassi di interesse dei principali paesi europei (Francia, Belgio, Spagna, Italia, Olanda) e quelli tedeschi a 10 anni;
- Euro/dollaro: tasso di cambio euro/dollaro;
- Spread US/GER 10Y: spread tra i tassi di interesse degli Stati Uniti e quelli tedeschi con scadenza 10 anni;
- Prezzo Oro: quotazione dell’oro (in USD)
- Spread 10Y/2Y Euro Swap Curve: differenza del tasso della curva EURO ZONE IRS 3M a 10Y e 2Y;
- Euribor 6M: tasso euribor a 6 mesi.
I colori sono assegnati in un’ottica VaR: se il valore riportato è superiore (inferiore) al quantile al 15%, il colore utilizzato è l’arancione. Se il valore riportato è superiore (inferiore) al quantile al 5% il colore utilizzato è il rosso. La banda (verso l’alto o verso il basso) viene selezionata, a seconda dell’indicatore, nella direzione dell’instabilità del mercato. I quantili vengono ricostruiti prendendo la serie storica di un anno di osservazioni: ad esempio, un valore in una casella rossa significa che appartiene al 5% dei valori meno positivi riscontrati nell’ultimo anno. Per le prime tre voci della sezione “Politica Monetaria”, le bande per definire il colore sono simmetriche (valori in positivo e in negativo). I dati riportati provengono dal database Thomson Reuters. Infine, la tendenza mostra la dinamica in atto e viene rappresentata dalle frecce: ↑,↓, ↔ indicano rispettivamente miglioramento, peggioramento, stabilità rispetto alla rilevazione precedente.
Disclaimer: Le informazioni contenute in questa pagina sono esclusivamente a scopo informativo e per uso personale. Le informazioni possono essere modificate da finriskalert.it in qualsiasi momento e senza preavviso. Finriskalert.it non può fornire alcuna garanzia in merito all’affidabilità, completezza, esattezza ed attualità dei dati riportati e, pertanto, non assume alcuna responsabilità per qualsiasi danno legato all’uso, proprio o improprio delle informazioni contenute in questa pagina. I contenuti presenti in questa pagina non devono in alcun modo essere intesi come consigli finanziari, economici, giuridici, fiscali o di altra natura e nessuna decisione d’investimento o qualsiasi altra decisione deve essere presa unicamente sulla base di questi dati.

Last 11 February 2019 the European Commission (EC) asked the European Insurance and Occupational Pension Authority (EIOPA) for a call for advice on the 2020 review of SII. As a response to that, EIOPA launched a public Consultation Paper (CP) on the 15th October 2019 whose feedback were to be submitted by the 15th January 2020 (Insurance and Reinsurance undertakings submitted their results to the NSAs last 6 December 2019, and the NSAs reported them to EIOPA last 8 January 2020). EIOPA is now collecting the data and assessing the impacts of its proposals, setting out the final advice by next 30th June 2020. The proposals presented are a view of EIOPA and may not be adopted: the EC will balance political considerations to the technical ones. It’s interesting to notice that EIOPA has reiterated in the CP its suggestion of introducing negative interest rates in the SF SCR calculation (advice dated 2018) previously rejected by the EC.
The call for advice comprised 19 topics, which can be broadly divided into three parts
- review of the Long Term Guarantee (LTG) measures, always foreseen as being reviewed in 2020, as specified in the Omnibus II Directive
- potential introduction of new regulatory tools in the SII Directive, notably on macro-prudential issues, recovery and resolution, and insurance guarantee schemes
- revisions to the existing SII framework, including reporting and disclosure of the SCR.
The main proposals set out in the CP and discussed in the following are:
- choose a later Last Liquid Point (LLP) for the extrapolation of risk-free interest rates for the Euro or change the extrapolation method to take into account market information beyond that point; these are expected to increase both TP and SCR, particularly for firms with long duration businesses
- change the calculation of the Volatility Adjustment (VA), to address overshooting effects and to reflect the illiquidity of insurance liabilities; 8 variations are proposed and, albeit they may help in reducing the volatility caused by the current design, they may increase the complexity of the calculation and even reduce the overall protection provided by this measure
- review the calibration of the interest rate risk sub-module in line with empirical evidence, considering negative interest rates; this is expected to increase the SCR
- include macro-prudential tools in the SII Directive and establish a minimum harmonised recovery and resolution framework for insurance.
No changes have been proposed for the Risk Margin (RM), causing the disappointment of many firms that consider this metric too big for the annuity business and too sensitive to interest rates changes – and therefore sensitive to the changes proposed to the LLP.
Positive and negative proposals have been made with respect to the Matching Adjustment (MA), currently only applied in Spain and UK. A good aspect is that EIOPA has proposed to recognize diversification between MA and non-MA portfolios, reducing the SCR, but without showing any intention to make the MA more flexible and adding a further requirement on restructured assets that may make it harder for the firms to apply the MA.
Regarding [A], EIOPA has proposed 5 options to amend the Euro LLP:
- no changes (i.e. LLP=20 years, Smith-Wilson extrapolation)
- LLP=20 + safeguards in terms of disclosure and governance
sensitivity analysis on LLP=50 to be include in the RSR and SFCR; if the firms breach the SCR or MCR in the sensitivity analysis, they have to provide evidences that the policy holders protection is not put at stake by dividend payments and capital distributions, which can be limited by the NSAs in case the evidences were not satisfying
- LLP=30 + safeguards in terms of disclosure and governance (as in option 2)
- LLP=50
- alternative extrapolation method to consider market data beyond the LLP for all the currencies
Beyond causing a detriment to the SCR position of the insurance firms, options from 2 to 4 are quite onerous.
Regarding [B], EIOPA has proposed a reform to the VA calculation that comprises 8 different design options, 3 different General Application Ratio (GAR), the usage of Dynamic VA (DA) under the SF and approval to the use of VA.
The presented options for the VA design are:
- “Undertaking-specific VA”, based on undertaking-specific asset weights and market spreads
- “Middle bucket” approach, where the current MA and VA approaches remain and the undertaking-specific VA is introduced as the middle bucket. Firms can only apply the middle bucket to insurance liability portfolios subject to meeting certain cash flow matching criteria.
- “Asset driven approach”: the VA would not be applied to the risk free curve. Instead, the VA would adjust the bond spreads on the asset side, where the difference in the value of bonds without and with the VA adjustment is recognised as an own funds item.
- Application ratio that takes into account of the undertaking’s AL mismatch. The proposed formula to derive the VA under this approach includes applying an asset liability (AL) mismatch ratio, where the ratio is calculated as the sensitivity of the BEL to the VA divided by the sensitivity of fixed income assets to the VA. Firms are also allowed to derive the risk-corrected spread using either the VA reference portfolio or their own specific fixed income portfolio (as under design option 1).
- Application ratio that takes into account of the undertaking’s illiquid liabilities. EIOPA suggests two approaches for this calculation: the first approach (paragraph 2.399) is similar to option 4 above, except that an illiquid liabilities ratio is applied; the second approach allocates liabilities to buckets of different levels of illiquidity with different application ratios.
- “Relative risk-corrections”: the risk correction is calculated as a fixed percentage of the spread.
- Amendment to the trigger and calculation of any country-specific increase of the VA.
- Create a “permanent VA” that reflects the long term illiquid nature of insurance cash-flows, and a “macro-economic VA” that will only exist when bond spreads are wide, e.g. during crisis. The macro-economic VA would replace the existing country specific add-on.
EIOPA has proposed 2 approaches based on a mix of these design options
APPROACH 1: permanent VA calculated as a combination of options 4, 5 and 6 and macroeconomic
VA based on option 8.
APPROACH 2: permanent VA calculated as a combination of options 1, 4 and 5.
The VA decreases in both approaches, but the latter is preferred by the industry as it produces a lower impact.
The 3 options presented for the GAR used in the VA calculation are:
- no changes (i.e. GAR= 65%), advised by EIOPA
- GAR = 100%
- GAR between 65% and 100%.
EIOPA advice for the DA was not to allow its usage under the SF as it would favour firms applying the SF versus those applying the IM, as the government bond risks are not fully captured in the SF.
EIOPA has highlighted that the need of a supervisory approval for the usage of VA should be consistent among all member states (it is currently required in 10 countries and not required in 17 others), but the Authority will decide on its preference after the consultation.
Regarding [C], EIOPA has confirmed its previous advice dated 2018 (relative shift approach), highlighting the need of modifying the IR risk calibration
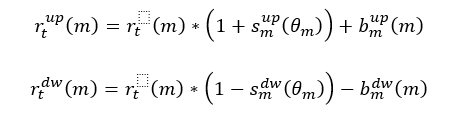
The 3-years gradual implementation period would be reviewed in light of the proposed changes on the Risk Free Rates reported in [A] and [B].
Regarding [D], EIOPA has proposed to introduce tools to address systemic risk in the insurance sector by adding a general article to the SII Directive, to achieve consistency and coherence with the micro-prudential approach. NSAs should have the power to set a capital surcharge to address sources of systemic risk, to define soft thresholds for action at market level if an exposure increases dramatically and to impose a temporary restriction on surrender rights for policyholders. NSAs can require systemic risk management plans and all firms should be required to draft liquidity risk management plans, unless they obtain a waiver. The ORSA principle will be changed to explicitly include macro-prudential concerns. EIOPA has also proposed to:
- require firms with a high market share to develop a recovery plan
- set an officially designated administrative resolution authority in each member state
- provide the NSAs with resolution powers of: prohibiting bonus payments to senior management; withdrawing the licence to write new business and put all or part of existing business into run-off; selling or transferring shares, assets and liabilities to third parties; restricting the rights of policyholders to surrender policies; suspending payments to unsecured creditors; until the point of taking control of the entity.



